DM à résoudre
14 messages
- Page 1 sur 1
DM à résoudre
Quelqu'un peut il m'aider a trouver la solution de cette énigme pour un DM ?
merci
Soit un nombre N de 6 chiffres commencant par 1. Si on fait passer ce 1 de l'extreme gauche a l'extreme droite, sans changer les autres chiifres, on lit alors un nombre egal au triple de N
merci
Soit un nombre N de 6 chiffres commencant par 1. Si on fait passer ce 1 de l'extreme gauche a l'extreme droite, sans changer les autres chiifres, on lit alors un nombre egal au triple de N
1....a = ....a1 x 3
si tu commences la multiplication par 3 tu auras 3x1 = 3 donc a est 3
alors le nombre s'écrit:
1...b3 = ....31 x 3
si tu continues la multiplication 3x3 = 9, alors b= 9
attention aux retenues à venir mais c'est pareil continue ce truc ...
si tu commences la multiplication par 3 tu auras 3x1 = 3 donc a est 3
alors le nombre s'écrit:
1...b3 = ....31 x 3
si tu continues la multiplication 3x3 = 9, alors b= 9
attention aux retenues à venir mais c'est pareil continue ce truc ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Avec a,b ... f entiers dans [0 ; 9]
N = 10^5 + 10^4.a + 1000.b + 100 c + 10d + f
N' = 10^5.a + 10^4.b + 1000c + 100d + 10f + 1
N' = 3N
10^5.a + 10^4.b + 1000c + 100d + 10f + 1 = 3.10^5 + 3.10^4.a + 3000.b + 300 c + 30d + 3f
3.10^5 - 70000a - 7000b - 700c - 70d - 7e -1 = 0
70000a + 7000b + 700c + 70d + 7e = 299999
10000a + 1000b + 100c + 10d + e = 42857
--> e = 7
10000a + 1000b + 100c + 10d = 42850
1000a + 100b + 10c + d = 4285 --> d = 5 , a = 4, b = 2 et c = 8
N = 142857
:zen:
N = 10^5 + 10^4.a + 1000.b + 100 c + 10d + f
N' = 10^5.a + 10^4.b + 1000c + 100d + 10f + 1
N' = 3N
10^5.a + 10^4.b + 1000c + 100d + 10f + 1 = 3.10^5 + 3.10^4.a + 3000.b + 300 c + 30d + 3f
3.10^5 - 70000a - 7000b - 700c - 70d - 7e -1 = 0
70000a + 7000b + 700c + 70d + 7e = 299999
10000a + 1000b + 100c + 10d + e = 42857
--> e = 7
10000a + 1000b + 100c + 10d = 42850
1000a + 100b + 10c + d = 4285 --> d = 5 , a = 4, b = 2 et c = 8
N = 142857
:zen:
Salut !
Si on note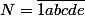 (écriture décimale de
(écriture décimale de  ) où
) où 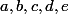 sont des chiffres, alors on a
sont des chiffres, alors on a 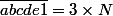 .
.
Maintenant, tu peux peut-être essayer de chercher une piste en exploitant par exemple le fait que :
[CENTER]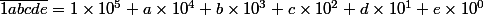 [/CENTER]
[/CENTER]
et de même,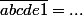 .
.
Ce n'est pas dit, mais il faut bien cherche ?
?
zozo06480 a écrit:Quelqu'un peut il m'aider a trouver la solution de cette énigme pour un DM ?
merci
Soit un nombre N de 6 chiffres commencant par 1. Si on fait passer ce 1 de l'extreme gauche a l'extreme droite, sans changer les autres chiifres, on lit alors un nombre egal au triple de N
Si on note
Maintenant, tu peux peut-être essayer de chercher une piste en exploitant par exemple le fait que :
[CENTER]
et de même,
Ce n'est pas dit, mais il faut bien cherche
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
on en était à a =7
si b est juste avant a = 7
alors reprends ta multiplication
tu dois faire
3xb + 2 (la retenue de 3x7= 21, je pose 1 retiens 2) = ...7
il faut faire du 3xb se termine par 5 (le 7-2)
c'est que b= 5
idem tu auras alors pour le suivant c
3xc + 1 (ta retenue du 15, je pose 5 je retiens 1) = ..5
il faut du 3xc qui fasse du 4 à la fin,
c'est 3x8 = 24 qui realise cela
and so on.
Si tu sais écrire en langage maths comme Black Jack c'est mieux.
Mais en sortant de primaire avec une multiplication posée en colonnes tu domines encore cet exo.
La force de l'ecole primaire est en toi ...Sors ton laser de CM1 ou 2 et bats toi...
si b est juste avant a = 7
alors reprends ta multiplication
tu dois faire
3xb + 2 (la retenue de 3x7= 21, je pose 1 retiens 2) = ...7
il faut faire du 3xb se termine par 5 (le 7-2)
c'est que b= 5
idem tu auras alors pour le suivant c
3xc + 1 (ta retenue du 15, je pose 5 je retiens 1) = ..5
il faut du 3xc qui fasse du 4 à la fin,
c'est 3x8 = 24 qui realise cela
and so on.
Si tu sais écrire en langage maths comme Black Jack c'est mieux.
Mais en sortant de primaire avec une multiplication posée en colonnes tu domines encore cet exo.
La force de l'ecole primaire est en toi ...Sors ton laser de CM1 ou 2 et bats toi...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
chan79 a écrit:salut
on cherche un nombre de la forme+A (A avec 5 chiffres)
on résout:
résultat:
NB: On pourra chercher la période de 1/7 et voir ce qu'il se passe quand on la multiplie par 2, par 3,...
Very nice Mr Chan79!Et bonne année 2016 à toi.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
