Un rectangle dans un triangle ???

[Julia11]

Bonsoir ?



Ce n'est pas dans mes habitudes de demander de l'aide mais là je ne comprend pas du tout alors auriez-vous la gentillesse de m'aider s'il vous plaît ?? :help:

Sur un schéma, ABC est un triangle rectangle tel que AB = 10 cm, AC = 6 cm et BC = 8 cm.
P est un point du segment [AB].
PQCS est un rectangle inscrit dans le triangle ABC.
On pose PQ = x

1.On appelle A(x) l'aire du rectangle PQCS en cm Carré.
Montrer que A(x) = moins quatre / tiers fois x au carre + 8x.

2. Calculer A de (un / quart).

Ce serait gentil de m'aider merci d'avance à bientôt j'espere !

[lu363]

Si tu fais une figure, tu vois que:
(On va dire que fois=x)

A(X)= SP x X

Or, SP parallèle à CB (car SPQC est un rectangle) et A,S,P et A,P,B sont alignés.
Tu appliques le théorème de Thalès : AS/AC = AP/AB = SP/CB
[suite supprimée par la modération - aider ne signifie pas donner la solution !!!]

[mathelot]

bonjour,

l'exercice est plutôt difficile. :hum:

1)
il semble qu'il y ait deux résultats différents si l'on suppose
(PQ) parallèle à (BC)
ou (PQ) parallèle à (AC).



içi, fais la figure avec

P est un point "mobile",on dit aussi "variable".

On peut poser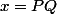 et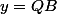

la tangente de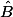 est constante, vaut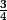

Du fait que cette tangente () est constante,

on peut calculer comme fonction linéaire de .
Quel est le coefficient de proportionalité ?
(c'est sûrement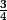 ou !!)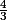

Ensuite et finalement,
la longueur QC se calcule aussi à l'aide de la variable

[oscar]

Bonjour

Figure


http://img140.imageshack.us/my.php?image=trianglessemblables2yn0.jpg

[oscar]

bonjour

figure


http://img140.imageshack.us/my.php?image=triangleszsemblables2up3.jpg

[oscar]

Triangles rectangles AQP et PSB semblables (1 angle =) P°oser PQ=x: PS =y
=> QP/PS = AQ/PS ou x/(8-x) = (6-y)/y
Produit en diagonales=xy = 48-8y-6x+xy
=> 8y = 48 - 6x
=> y = 6 - 3/4 x
Donc A(x) = x*y = x*( 6- 3/4x)ou -4/3 y² +8y