Racine carrée [3ème]
Réponses à toutes vos questions du CP à la 3ème
-
mathelot
 par mathelot » 01 Sep 2010, 21:12
par mathelot » 01 Sep 2010, 21:12
mathelot a écrit:Simplifier
\left( \sqrt{1}+\sqrt{2}-\sqrt{3} \right)\left( \sqrt{2}+\sqrt{3}-\sqrt{1} \right)\left( \sqrt{1}+\sqrt{3}-\sqrt{2} \right)})
Celle là est inspirée de la formule d'aire d'un triangle de Héron,
que vous verrez en 1ère.
avec l'identité (A+B)(A-B)
\left( \sqrt{1}+\sqrt{2}-\sqrt{3} \right)=\left( \sqrt{1}+\sqrt{2} \right)^2 - 3)
avec l'identité
^2)
\left( \sqrt{1}+\sqrt{2}-\sqrt{3} \right)=3+2 \sqrt{2} - 3)
De même
\left( \sqrt{1}+\sqrt{3}-\sqrt{2} \right)=3-\left(\sqrt{2}-\sqrt{1} \right)^2=3-\left(3 - 2 \sqrt{2} \right))
au final
\left( \sqrt{1}+\sqrt{2}-\sqrt{3} \right)\left( \sqrt{2}+\sqrt{3}-\sqrt{1} \right)\left( \sqrt{1}+\sqrt{3}-\sqrt{2} \right)}=2 \sqrt{2})
-
mathelot
 par mathelot » 01 Sep 2010, 21:20
par mathelot » 01 Sep 2010, 21:20
re-bonjour,
On pose
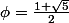

se prononce "phi"
Montrer que
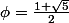
est racine de l'équation
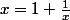
En déduire la valeur de la fraction

-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 02 Sep 2010, 10:12
par Euler07 » 02 Sep 2010, 10:12
C'est même la racine positif de l'équation
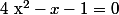
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 02 Sep 2010, 18:00
par oscar » 02 Sep 2010, 18:00
Bonjour
V ( 2 ^ 100 + 2 ^51 +1) = V ( 2 ^100 +2 +2^50 +1)
On a un produit remarquable!
-
mathelot
 par mathelot » 03 Sep 2010, 04:30
par mathelot » 03 Sep 2010, 04:30
mathelot a écrit:Bonjour,
Simplifier

:we:
Bonjour à tous !
^2=a^4=a^{2 ^2 })
on s'autorise à écrire une formule à la place de l'exposant...
on continue
^2=a^{2 ^2 \times 2 }=a^{2 ^3 })
Quand on élève

à la puisssance 8, on élève

trois fois de suite au carré
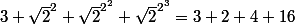
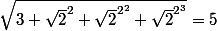
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités