Racine carrée (défi classe de 3ème)
Réponses à toutes vos questions du CP à la 3ème
 par busard_des_roseaux » 16 Aoû 2009, 09:27
par busard_des_roseaux » 16 Aoû 2009, 09:27
bonjour,
je vous propose le défi suivant:
Montrer l'égalité:
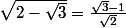
@+++
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 16 Aoû 2009, 10:52
par oscar » 16 Aoû 2009, 10:52
Bonjour
Il suffit d' élever au carré les deux membres ( Attention aux conditions...)
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 16 Aoû 2009, 11:01
par Euler911 » 16 Aoû 2009, 11:01
Bonjour,
Heureusement, Oscar, que le titre de ce fil signale qu'il s'agit d'un défi destiné à des 3e...
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 16 Aoû 2009, 11:43
par Clembou » 16 Aoû 2009, 11:43
On peut tout de même donner des indications (but du forum) tout en ne donnant pas la réponse entière :++:
 par busard_des_roseaux » 16 Aoû 2009, 12:08
par busard_des_roseaux » 16 Aoû 2009, 12:08
hint: découvrir une identité remarquable cachée
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 06:49
par Zweig » 17 Aoû 2009, 06:49
Indice 2 :
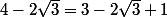
-
mathelot
 par mathelot » 18 Aoû 2009, 12:23
par mathelot » 18 Aoû 2009, 12:23
Zweig a écrit:Indice 2 :
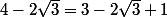
alors, vous avez obtenu l'identité remarquable ?
-
mathelot
 par mathelot » 20 Aoû 2009, 11:19
par mathelot » 20 Aoû 2009, 11:19
Zweig a écrit:Indice 2 :
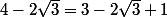
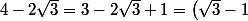^2)
là, c'est gagné. on a un carré parfait.
 par busard_des_roseaux » 21 Aoû 2009, 02:59
par busard_des_roseaux » 21 Aoû 2009, 02:59
busard_des_roseaux a écrit:Montrer l'égalité:
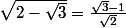
l'égalité équivaut à
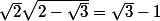
en multipliant par

les deux membres de l'égalité
or le membre de gauche vaut:
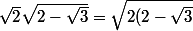}=\sqrt{4-2\sqrt{3}})
la quantité
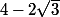
,sous la racine, est le carré de:
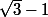
d'où
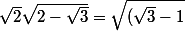^2})
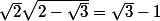
car
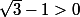
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités