Problèmes mathématiques
13 messages
- Page 1 sur 1
Problèmes mathématiques
Bonsoir,
Depuis tout à l'heure, je me suis mis à résoudre quelques problèmes mathématiques que le prof nous a proposés. J'ai pu en résoudre quelques uns, mais je galère pour les autres. Qui sont, par ailleurs, deux :
Voici les énoncés :
Problème 1 : Un champ de la forme d'un rectangle a pour périmètre 110m. Si on ajoute 1m à sa longueur et on soustrait 1m de sa largeur, sa superficie diminue de 4m^2.
Trouve les dimensions de ce champ.
Problème 2 : Trois disques sont différents, sachant que le rayon du plus grand disque dépasse le rayon du disque moyen de 2, et le rayon du petit disque a 2 en moins que celui du disque moyen.
Calcule le rayon du petit disque sachant que la superficie du plus grand disque est égale au total des deux superficies des autres disques.
Voilà, je vous prie de bien vouloir m'aider. Et bonne soirée.
Depuis tout à l'heure, je me suis mis à résoudre quelques problèmes mathématiques que le prof nous a proposés. J'ai pu en résoudre quelques uns, mais je galère pour les autres. Qui sont, par ailleurs, deux :
Voici les énoncés :
Problème 1 : Un champ de la forme d'un rectangle a pour périmètre 110m. Si on ajoute 1m à sa longueur et on soustrait 1m de sa largeur, sa superficie diminue de 4m^2.
Trouve les dimensions de ce champ.
Problème 2 : Trois disques sont différents, sachant que le rayon du plus grand disque dépasse le rayon du disque moyen de 2, et le rayon du petit disque a 2 en moins que celui du disque moyen.
Calcule le rayon du petit disque sachant que la superficie du plus grand disque est égale au total des deux superficies des autres disques.
Voilà, je vous prie de bien vouloir m'aider. Et bonne soirée.
Re: Problèmes mathématiques
Bonsoir,
Problème 1 : Un champ de la forme d'un rectangle a pour périmètre 110m.
2.(L+l) = 110
Si on ajoute 1m à sa longueur et on soustrait 1m de sa largeur, sa superficie diminue de 4m^2.
(L+1)(l-1)= avec S=L.l
avec S=L.l
==============> Trouve les dimensions de ce champ., c'est-à-dire L et l
Problème 1 : Un champ de la forme d'un rectangle a pour périmètre 110m.
2.(L+l) = 110
Si on ajoute 1m à sa longueur et on soustrait 1m de sa largeur, sa superficie diminue de 4m^2.
(L+1)(l-1)=
==============> Trouve les dimensions de ce champ., c'est-à-dire L et l
Re: Problèmes mathématiques
Merci de votre réponse.
Donc cela me donnerait :
L.l - L + l - 1 = S - 4
S - L + l - 1 = S - 4
S - S + l - L = -4 +1
On sait que L + l = 110 donc l = 110 - L
l - L = -3
110 - 2L = -3
-2L = -113
L = 113/2
Mais je ne vois pas à quoi le périmètre va me servir et j'arrive pas vraiment à résoudre l'équation.
Donc cela me donnerait :
L.l - L + l - 1 = S - 4
S - L + l - 1 = S - 4
S - S + l - L = -4 +1
On sait que L + l = 110 donc l = 110 - L
l - L = -3
110 - 2L = -3
-2L = -113
L = 113/2
Mais je ne vois pas à quoi le périmètre va me servir et j'arrive pas vraiment à résoudre l'équation.
Re: Problèmes mathématiques
L = 113/2
Mais je ne vois pas à quoi le périmètre va me servir (si tu te sert d'une seule équation à 2 inconnues tu ne trouvera jamais, il faut te servir des 2 ====> résoudre un système de 2 équations à 2 inconnues) et j'arrive pas vraiment à résoudre l'équation.
C'est très bien, tu as cherché mais il doit y avoir une erreur quelque part . . .
regarde . . .
(L+1)(l-1) = Ll - 4
Ll - L + l - 1 - Ll = - 4
-L + l -1 = -4
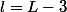
2L + 2l = 110
2L + 2(L-3) = 110
2L + 2L - 6 = 110
4L = 116


Vérification (toujours V E R I F I E R) :
p = 2(29+26) = 110 OK
(29+1)(26-1) = 29.26 - 4 = 750 OK
Bonne soirée.
Mais je ne vois pas à quoi le périmètre va me servir (si tu te sert d'une seule équation à 2 inconnues tu ne trouvera jamais, il faut te servir des 2 ====> résoudre un système de 2 équations à 2 inconnues) et j'arrive pas vraiment à résoudre l'équation.
C'est très bien, tu as cherché mais il doit y avoir une erreur quelque part . . .
regarde . . .
(L+1)(l-1) = Ll - 4
Ll - L + l - 1 - Ll = - 4
-L + l -1 = -4
2L + 2l = 110
2L + 2(L-3) = 110
2L + 2L - 6 = 110
4L = 116
Vérification (toujours V E R I F I E R) :
p = 2(29+26) = 110 OK
(29+1)(26-1) = 29.26 - 4 = 750 OK
Bonne soirée.
Re: Problèmes mathématiques
Problème 2 :
Je pense que ce petit croquis (pas à l'échelle) peut t'aider :
http://www.cjoint.com/c/FBysZW421V7
Donne-nous stp tes résultats pour valider . . .
Je pense que ce petit croquis (pas à l'échelle) peut t'aider :
http://www.cjoint.com/c/FBysZW421V7
Donne-nous stp tes résultats pour valider . . .
Modifié en dernier par laetidom le 24 Fév 2016, 19:52, modifié 1 fois.
Re: Problèmes mathématiques
Oh oui, je vois. Merci beaucoup.
Pour la deuxième, je crois que je devrai choisir le rayon du petit disque comme inconnu. Et je pourrais en déduire que x + 2 est le rayon du disque moyen et celui du grand est x + 4.
Cela me donnerait (pi).(x+4)^2 = (pi).(x+2)^2 + (pi).x^2
Est-ce que l'équation que j'ai posé est juste ?
Pour la deuxième, je crois que je devrai choisir le rayon du petit disque comme inconnu. Et je pourrais en déduire que x + 2 est le rayon du disque moyen et celui du grand est x + 4.
Cela me donnerait (pi).(x+4)^2 = (pi).(x+2)^2 + (pi).x^2
Est-ce que l'équation que j'ai posé est juste ?
Re: Problèmes mathématiques
sakuracce a écrit:Oh oui, je vois. Merci beaucoup.
Pour la deuxième, je crois que je devrai choisir le rayon du petit disque comme inconnu. Et je pourrais en déduire que x + 2 est le rayon du disque moyen et celui du grand est x + 4.
Cela me donnerait (pi).(x+4)^2 = (pi).(x+2)^2 + (pi).x^2
Est-ce que l'équation que j'ai posé est juste ?
Bonsoir,
Ca me parait juste ! et donc
Re: Problèmes mathématiques
En fait, j'arrive pas vraiment à la résoudre. En essayant, j'ai trouvé : (pi).(x^2 -4x-12) = 0
Re: Problèmes mathématiques
sakuracce a écrit:En fait, j'arrive pas vraiment à la résoudre. En essayant, j'ai trouvé : (pi).(x^2 -4x-12) = 0
Très bien ! sauf que
donc on aboutit à
je ne sais plus en quelle classe tu es,
si en première/terminale : tu connais le discriminant ....
vérif :
jusqu'à la seconde :
d'où :
enfin :
un petit visuel pour finir : http://www.cjoint.com/c/FByuDoHPMw7
Bonne soirée.
Re: Problèmes mathématiques
Merci énormément.
Par contre, comme j'ai factorisé avec pi, je doute que je puisse l'éliminer. Du moins, pas avec la démarche que j'ai suivie lors de la résolution de l'équation.
Par ailleurs, je suis en 3ème.
Merci encore.
Par contre, comme j'ai factorisé avec pi, je doute que je puisse l'éliminer. Du moins, pas avec la démarche que j'ai suivie lors de la résolution de l'équation.
Par ailleurs, je suis en 3ème.
Merci encore.
Re: Problèmes mathématiques
sakuracce a écrit:Merci énormément.
Par contre, comme j'ai factorisé avec pi, je doute que je puisse l'éliminer. Du moins, pas avec la démarche que j'ai suivie lors de la résolution de l'équation.
Par ailleurs, je suis en 3ème.
Merci encore.
Bonjour,
je te remets le début du calcul :
. . .
Bonne journée.
Re: Problèmes mathématiques
Je ne sais vraiment pas comment vous remercier. Mais je vais me contenter d'un "merci énormément" même si ce n'est pas assez.
Vous m'avez apportée beaucoup d'aide, sans vous je ne saurais comment faire.
Merci encore.
Je vous souhaite une excellente journée !
Vous m'avez apportée beaucoup d'aide, sans vous je ne saurais comment faire.
Merci encore.
Je vous souhaite une excellente journée !
Re: Problèmes mathématiques
sakuracce a écrit:Je ne sais vraiment pas comment vous remercier. Mais je vais me contenter d'un "merci énormément" même si ce n'est pas assez.
Vous m'avez apportée beaucoup d'aide, sans vous je ne saurais comment faire.
Merci encore.
Je vous souhaite une excellente journée !
J'ai été bien content de pouvoir t'aider, c'est très gratifiant de construire une correction / rédaction d'exercice E N S E M B L E comme ce fût le cas avec toi ! On n'a pas toujours cette réciprocité donc quand elle est présente, on apprécie amplement ! et c'est pour cela que moi aussi je te remercie une nouvelle fois !
Te souhaitant aussi une journée excellente et une bonne fin de vacances, @+ sur le forum.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
