Problème

[rfgauss]

Bonsoir,
Merci de m'aider à résoudre ce problème
Arnold possède une somme d'argent qui lui permet d'acheter soit 40 chemises soit 10 vestes soit 24 pantalons. Mais Arnold a décidé d'acheter avec cette somme d'argent un nombre de costumes: le costume est composé d'une chemise, d'un pantalon et d'une veste.
Déterminer le nombre de costumes que peut acheter Arnold avec cette somme d'argent

Merci beaucoup

[mathelot]

bonsoir,
il s'agit de mettre l'énoncé en équation. Quelles inconnues choisis tu ? quel va être le prix d'un costume ?

[mathelot]

soit x la somme d'argent.

que vaut une chemise en fonction de x ? (le prix d'une chemise peut se calculer avec une formule avec x)

[rfgauss]

Bonsoir, mathelot
le prix d'une chemise en fonction de est :

[mathelot]

Quel est le prix d'une veste (toujours en fonction de x) ?

d'un pantalon ?

enfin, d'un costume ?

[rfgauss]

Quel est le prix d'une veste (toujours en fonction de x) ?

d'un pantalon ?

enfin, d'un costume ?

de même le prix d'une veste en fonction de est : et le prix d'un pantalon en fonction de est :

Et je crois qu'on peut dire que : . c'est ca ?

[mathelot]

Réduis au même dénominateur et fais l'addition

[Black Jack]

Quel est le prix d'une veste (toujours en fonction de x) ?

d'un pantalon ?

enfin, d'un costume ?

de même le prix d'une veste en fonction de est : et le prix d'un pantalon en fonction de est :

Et je crois qu'on peut dire que : . c'est ca ?

Pas vraiment.

Cela te donnerait (en simplifiant par x dans les 2 membres) 1 = 1/24 + 1/10 + 1/40 ... ce qui n'est évidemment pas vrai.

Soit c le prix d'une chemise, p le prix d'un pantalon et v le prix d'une veste, on a :

40 c = 10 v = 24 p = S (avec S la somme dépensée)
--> c = S/40 ; v = S/10 ; p = S/24

Soit N le nombre de costumes, on a :
N * (c + v + p) = S
N * (S/40 + S/10 + S/24) = S
N * (1/40 + 1/10 + 1/24) = 1

Et maintenant tu peux calculer N le nombre de costumes.

[mathelot]

Le prix d'un costume est de :



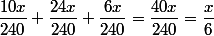
combien de costumes peut on acheter avec la somme (d'argent) x ?

[rfgauss]

Quel est le prix d'une veste (toujours en fonction de x) ?

d'un pantalon ?

enfin, d'un costume ?

de même le prix d'une veste en fonction de est : et le prix d'un pantalon en fonction de est :

Et je crois qu'on peut dire que : . c'est ca ?

Pas vraiment.

Cela te donnerait (en simplifiant par x dans les 2 membres) 1 = 1/24 + 1/10 + 1/40 ... ce qui n'est évidemment pas vrai.

Soit c le prix d'une chemise, p le prix d'un pantalon et v le prix d'une veste, on a :

40 c = 10 v = 24 p = S (avec S la somme dépensée)
--> c = S/40 ; v = S/10 ; p = S/24

Soit N le nombre de costumes, on a :
N * (c + v + p) = S
N * (S/40 + S/10 + S/24) = S
N * (1/40 + 1/10 + 1/24) = 1

Et maintenant tu peux calculer N le nombre de costumes.

Merci infiniment Black Jack, c'est trés clair

Le prix d'un costume est de :



combien de costumes peut on acheter avec la somme (d'argent) x ?

On peut en acheter 6. Merci beaucoup mathelot