Problème Pythagore

[Lubinos]

Bonjour,

Je suis étudiant en 4ème et je galère enormement sur cet exercice:


eric part en mer laissant marie son amoureuse éplorée sur la plage. Dans sa barque il rame en reculant pour qu'ils puissent rester se regarder les yeux dans les yeux. Au bout de combien de temps leurs regard ne pourront-ils plus se croiser?

Quelques informations :
Les yeux d'Eric sont à 1 mètre au dessus de l'eau
Les yeux de Marie sont a 1,7 mètre au dessus de l'eau
Les yeux de Marie sont verts et ceux d'Eric sont bleus
Eric se déplace a 2 mètre par seconde
La barque pèse 110 kg
Le rayon de la Terre est de 6371 km.

[qaterio]

Je penses, mais c'est mon avis, qu'il y a des informations inutiles, Eric se déplace dans quelle direction ?

[Lubinos]

eric se déplace vers le large et oui il y a des infos inutile comme la couleur des yeux ou le poids de la baque mais meme en éliminant ces infos je galère toujours

[qaterio]

fais-toi un schéma avec des points, et tu les nommes, puis tu écris les distances importantes.

[Lubinos]

on a déja essayer avec les pions d'un collège en perm mais ca n'a rien donné que des mauvaises pistes la seule que nous avons trouvés c'est que le gars rame 112 km pendant 14 heures un peu tirer par les cheveux

[WillyCagnes]

bjr

l'amoureuse ne verra plus Lubinos au bout de 29mn26s...

[Lubinos]

comment avez-vous fait créature °___°
Je rigole

[WillyCagnes]

mon calcul du temps correspond où l"amoureuse ne voit plus du tout Eric (ses orteils)
prends ton compas, trace un cercle de centre O , trace un rayon +1,7m et nomme le sommet le pt A (somme t de l'amoureuse)
puis trace la droite tangente au cercle au pt B;
observe donc un triangle rectangle ABO, et il faut connaitre l'angle au centre AOB grâce à un cos()
puis tu calcules l'ARC AB du cercle (revoir ton cours en fonction du Rayon)
et le temps (s) = distance de l'arc (m)/vitesse (m/s)

[Ben314]

Salut,
Perso, j'aurais fait (un tout petit peu) différemment de ce que fait Willy Cagnes :
Au départ tu as un cercle de centre et de rayon (=rayon terrestre) et deux points 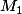et 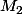à l'extérieur du cercle situés "à des altitudes 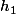(=1,7 mètre) et 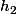(=1 mètre)", c'est à dire tels que 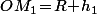et .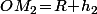
La question, c'est de savoir si le segment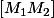 coupe le cercle ou pas : si oui, c'est qu'il ne peuvent plus se voir du fait que la "montagne virtuelle" que fait l'arrondi terrestre fait obstacle.
Ensuite, ce qu'il faut voir sur le dessin, c'est que le cas "limite" où ils peuvent encore se voir, c'est lorsque le segment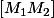 est tangent au cercle en un certain point (au delà, ils ne se voient plus).
Normalement, ce qu'il faudrait calculer dans ce cas là (et c'est ce que dit Willy Cagnes), c'est la longueur de l'arc de cercle allant de l'intersection de avec le cercle jusqu'à l'intersection de avec le cercle vu que c'est la distance parcourue par la barque (qui, elle, reste tout le temps à une altitude de 0).
Sauf qu'à mon avis, ce que tout le monde calcule dans un cas pareil, c'est plutôt directement la distance (en ligne droite) de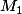 à 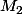vu que c'est bien plus simple à calculer et que, à un poil de c.. près, c'est la même chose (*).
Et cette distance, c'est la distance de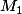 à plus la distance de à 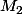qui se calculent facilement (et avec la même formule) vu que les triangles et sont rectangles en (la tangente à un cercle en un point donné est perpendiculaire au rayon) et que dans ces triangles on connaît deux des longueurs sur les 3.

(*) Ce qu'on peut éventuellement vérifier par du calcul si on sait comment calculer des longueurs d'arc de cercles.

P.S. Et pour ceux que ça intéresse, il y a une formule simple et bien connue des marins qui donne une très bonne approximation de la distance de à en fonction de la hauteur du point (formule bien évidement valable pour très petit devant le rayon terrestre )