[résolu]Problème de parallélisme

[Frednight]

Bonjour à tous

je rencontre un petit problème concernant la démonstration du parallélisme entre deux droites concernant la figure suivante :


Je souhaite démontrer que les droites AC et P1P3 sont parallèles en sachant que SA et CP sont parallèles de même que les droites SC et AP

Voilà je n'y parviens pas. Je suis pas loin de trouver la solution mais à chaque fois je finis par bloquer. J'ai essayé de passer par Thalès, les angles ou encore le parallélogramme ASCP.
Toute aide est la bienvenue

Merci d'avance

[Teamynil]

Essaie p'tete avec le parallélogramme P1P3CA, en démontrant que c'est un parallélogramme les deux droites seront donc parallèles, j'ai pas trop d'idée sur ce coup là ^^

[chan79]

salut
Je suppose qu'il faut lire B au lieu de C.
PASB est un parallélogramme.
Montre que SB/SP3=SA/SP1
Pour cela, utilise Thalès dans SP2P3 et SP1P2

[chan79]

Essaie p'tete avec le parallélogramme P1P3CA, en démontrant que c'est un parallélogramme les deux droites seront donc parallèles, j'ai pas trop d'idée sur ce coup là ^^

salut
On peut raisonner avec une figure fausse ...

si on mène par I la parallèle à (P1P3), on obtient la droite (AB) car sinon on ferait apparaître un quadrilatère ADBE qui serait un parallélogramme (c'est facile de montrer que ID=IE) dont les côtés opposés (DA) et (BE) se coupent en S.
----------------------------
On peut aussi le faire en plaçant par exemple le repère (P1,P2,S)
On prend P(a,1-a) sur (SP2) (à noter que l'équation de (SP2) est x+y=1)
Les équations des droites sont faciles à trouver:
(PB): x=a
(SP3): y=-x/2 + 1
(PA): y=-x/2 + 1-a/2
On obtient: A(0, 1 - a/2) et B(a, 1- a/2)

donc a comme coordonnées (a,0) d'où le parallélisme demandé

[Frednight]

J'ai trouvé comment le faire avec Thalès :
Supposons que ce que l'on doit prouver, c'est à dire que (AC) et () sont parallèles, soit vrai.
On a alors en appliquant respectivement le théorème de Thalès dans les triangles et notamment les égalités suivantes :


Or du fait du parallélisme de avec et avec , le quadrilatère est un parallélogramme dont les diagonales se coupent en leurs milieux d'où BC=AB ce qui me permet d'établir d'après l'égalité précédente que celle-ci équivaut donc à :


Or, cette égalité est forcément vraie sans que l'on ait besoin de faire l'hypothèse que (AC) et () sont parallèles, puisque elle est donnée en énoncé. Par réciprocité, on en déduit donc que (AC) et () sont forcément parallèles.

[Frednight]

En tout cas merci beaucoup pour votre aide, surtout toi Chan :we:

[chan79]

J'ai trouvé comment le faire avec Thalès :
Supposons que ce que l'on doit prouver, c'est à dire que (AC) et () sont parallèles, soit vrai..

salut
Tu devrais reprendre ta démo, je crois. Si tu supposes que ce que tu veux démontrer est vrai, tu vas forcément le prouver... ou alors il faut s'exprimer d'une autre manière. Cet exo n'est pas simple, finalement

[Frednight]

salut
Tu devrais reprendre ta démo, je crois. Si tu supposes que ce que tu veux démontrer est vrai, tu vas forcément le prouver... ou alors il faut s'exprimer d'une autre manière. Cet exo n'est pas simple, finalement

Je ne comprends pas en quoi cela peut rendre ma démonstration fausse...?
Si ma supposition est équivalente à quelque chose de vrai, ce que j'ai démontré, pourquoi ne serait-elle pas vraie également?

[Faraziel]

Justement tu démontre pas l'équivalence, ce que tu fais c'est que tu démontre que si (AC) // à P1P2 implique P1P2=P2P3, mais pas que P1P2=P2P3 implique (AC) // à P1P2.

Le tout est à démonter avec les règles de construction qui sont donner.

il suffit de voir la table des vérité de l’implication pour s'en rendre compte :

P Q P ;) Q Q ;) P (réciproque)
V V V V
V F F V
F V V F
F F V V

Ici P est l'assertion P1P2=P2P3, qui est vrai par construction.
et Q l’assertion P1P2 // à (AC), qui ici reste à démontrer et qui est donc ni vrai ni fausse.

[Frednight]

Justement tu démontre pas l'équivalence, ce que tu fais c'est que tu démontre que si (AC) // à P1P2 implique P1P2=P2P3, mais pas que P1P2=P2P3 implique (AC) // à P1P2.

Le tout est à démonter avec les règles de construction qui sont donner.

il suffit de voir la table des vérité de l’implication pour s'en rendre compte :

P Q P Q Q P (réciproque)
V V V V
V F F V
F V V F
F F V V

Ici P est l'assertion P1P2=P2P3, qui est vrai par construction.
et Q l’assertion P1P2 // à (AC), qui ici reste à démontrer et qui est donc ni vrai ni fausse.

ah oui effectivement je suis allé un peu vite en besogne...

[Frednight]

Je pense avoir trouvé une nouvelle façon qui est juste cette fois-ci.
Etape 1
D'abord considérons une nouvelle figure : http://speedy.sh/HEbzA/triangle.png
Soient trois points A, B et C.
On trace les droites (AB) et (AC) ainsi que la médiane (AD) du triangle ABC
On trace une droite quelconque coupant respectivement (AB), (AD) et (AC) en F, E et G et telle que FE=EG.
On cherche à démontrer que (BC) et (FG) sont parallèles en ayant pour seul élément que (AD) est la médiane des triangles ABC et AFG

On établit qu'il existe tels que :


On a alors d'après ces égalités :


Or comme et que et ne sont pas colinéaires, cela induit donc que :



Ce qui induit :


Et donc finalement que (BC) et (FG) sont parallèles
Ainsi, deux triangles imbriqués ayant un même sommet en commun ainsi que la même médiane partant ce sommet, alors leurs bases opposées à ce sommet sont parallèles.

Etape 2 :
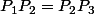
En observant la figure http://speedy.sh/GgV7M/image.png, on constate que comme donné en énoncé et que du fait que SAPC soit un parallélogramme, AB=BC.
Cela correspond exactement à la me^me configuration que vu précédemment, donc les droites () et (AC) sont parallèles

---------------------------------------------

Qu'en pensez-vous?

[chan79]

On trace une droite parallèle à (BC) coupant respectivement (AB), (AD) et (AC) en F, E et G.


Et donc finalement que (BC) et (FG) sont parallèles

Salut
Je crois que tu as "démontré" quelque chose qui était déjà dans tes hypothèses

[Frednight]

Salut
Tu crois que tu as "démontré" quelque chose qui était déjà dans tes hypothèses

J'ai corrigé mon énoncé : on ne prend en aucun cas comme hypothèses que les droites (BC) et (FG) sont parallèles

[Ben314]

Salut,
Si désigne le symétrique de par rapport à alors est un parallélogramme vu que ces diagonales se coupent en leur milieu.
L'homothétie de centre telle que envoie la droite sur une droite passant par et parallèle à donc parallèle à .
C'est donc la droite et cela montre que .
De même et on en déduit évidement que

P.S. : j'ai pas fait gaffe qu'on était dans "collège" : je suis pas sûr qu'ils aient vu les homothéties... (on peut sans doute s'en passer en utilisant Thalés, mais ça risque d'être moins naturel)

[Frednight]

De même

C'est pas plutôt?

P.S. : j'ai pas fait gaffe qu'on était dans "collège" : je suis pas sûr qu'ils aient vu les homothéties... (on peut sans doute s'en passer en utilisant Thalés, mais ça risque d'être moins naturel)

Non c'est moi qui ait fait la boulette en postant ce topic dans la rubrique collège vu que je pensais que c'était résolvable avec Thalès sans problème, mes difficultés ne tenant qu'à un détail.
Pour le coup, mes tentatives de résolution avec Thalès ont manqué de peu de me rendre fou ^^

En tout cas merci pour ton aide

[Ben314]

C'est pas plutôt?

Non, c'est bien : , et le centre de l'homothétie ne sont pas alignés...

[Frednight]

Non, c'est bien : , et le centre de l'homothétie ne sont pas alignés...

Sur quelle figure as-tu raisonné? celle que j'ai donnée au début ou celle de Chan79?

Si c'est la mienne j'arrive à te suivre jusqu'à l'avant dernière ligne de ta démonstration mais après je n'y comprends plus rien...

[Frednight]

Salut,
Si désigne le symétrique de par rapport à alors est un parallélogramme vu que ces diagonales se coupent en leur milieu.
L'homothétie de centre telle que envoie la droite sur une droite passant par et parallèle à donc parallèle à .
C'est donc la droite et cela montre que .
De même et on en déduit évidement que

P.S. : j'ai pas fait gaffe qu'on était dans "collège" : je suis pas sûr qu'ils aient vu les homothéties... (on peut sans doute s'en passer en utilisant Thalés, mais ça risque d'être moins naturel)

En fait je comprends ton raisonnement mais je pense que l'on a pas travaillé sur la même figure d'où ma confusion :


En tout cas merci beaucoup pour ta démonstration concise et efficace :id:

[Frednight]

J'aurais une autre question basée sur la figure suivante :


Dans le triangle AA'B', j'observe que B'C est une de ses médianes et que (AB) coupe celle-ci au tiers en partant de sa base. Est-ce suffisant pour affirmer que AD est donc également la médiane de AA'B'?

[mouette 22]

si tu sais par hypothèse que A'C=CA , B'C est donc une médiane

si toujours par hypothèse CB=BC'=C'B' , B est donc le centre de gravité du triangle et donc ça implique que AD est une médiane .