Bonjour,
Ma fille a ce problème :
Des enfants ramassent entre 62 et 104 œufs.
S'ils les rangent dans des boîtes de 6 ou 10 œufs, chaque fois, il leur en reste 5.
Recherche combien ils en ont ramassé précisément.
(2 solutions).
Alors, par tâtonnement, j'arrive à trouver 65 et 95 (si je ne fais pas d'erreur) qui vérifient l'énoncé.
Mais pas moyen de trouver ces réponses mathématiquement en écrivant une équation...
Une idée ?
Je suis en train de me prendre la tête dessus et pas moyen de lui expliquer correctement....
Merci d'avance.
Petit problème
13 messages
- Page 1 sur 1
Re: Petit problème
Bon, de tête je dirais que c'est en résolvant l'équation:
3x-5y=0, et dès que vous avez résolu cette équation vous prenez les valeurs telles que 3x+5 soit compris entre 62 et 104. Mais c'est plutôt niveau terminale S ces équations, je pense qu'il fallait le faire en tatônnant comme vous l'avez fait.
L'équation 3x-5y=0 vient de 6x+5=10y+5, soit 6x-10y=0, soit 3x-5y=0.
3x-5y=0, et dès que vous avez résolu cette équation vous prenez les valeurs telles que 3x+5 soit compris entre 62 et 104. Mais c'est plutôt niveau terminale S ces équations, je pense qu'il fallait le faire en tatônnant comme vous l'avez fait.
L'équation 3x-5y=0 vient de 6x+5=10y+5, soit 6x-10y=0, soit 3x-5y=0.
Re: Petit problème
En faite, si x est pas un multiple de 5, y'a pas de solutions. Donc ça permet de faire avancer plus vite les possibilités de solutions si on cherche pas à déterminer l'ensemble des solutions, qui n'est pas bien compliqué.
Re: Petit problème
(pour info elle est en 2° secondaire en Belgique, équivalent 4° Collège en France)
Re: Petit problème
Donc il n'est pas possible de poser une équation pour trouver les résultats dans l'intervalle demandé ?
Re: Petit problème
On cherche X tel que
X=10x+5
et
X=6y+5
(avec x et y des entier strictement positifs)
Voilà, comme ça j'ai tout détaillé comment on en arrive à 3x-5y=0.
X=10x+5
et
X=6y+5
(avec x et y des entier strictement positifs)
Voilà, comme ça j'ai tout détaillé comment on en arrive à 3x-5y=0.
Re: Petit problème
Personnellement, pour un 4ème, je vois pas comment elle pourrait faire.
Enfin, ce qu'elle pourrait faire, c'est choisir X=65, X=75, X=85 et X=95 et résoudre le système ci-dessus.
Enfin, ce qu'elle pourrait faire, c'est choisir X=65, X=75, X=85 et X=95 et résoudre le système ci-dessus.
Modifié en dernier par qaterio le 07 Oct 2018, 12:19, modifié 1 fois.
Re: Petit problème
OK... c'est bien ce que je pensais.
Mais je voulais avoir confirmation.
Merci beaucoup
Mais je voulais avoir confirmation.
Merci beaucoup
Re: Petit problème
Unrender a écrit:Bonjour,
Ma fille a ce problème :
Des enfants ramassent entre 62 et 104 œufs.
S'ils les rangent dans des boîtes de 6 ou 10 œufs, chaque fois, il leur en reste 5.
Recherche combien ils en ont ramassé précisément.
(2 solutions).
Bonjour,
Voici une méthode du niveau collège.
Le but est de trouver le nombre d'oeufs ramassés.
Comme ce nombre est inconnu, appelons-le N.
N est donc un nombre compris entre 62 et 104 d'après l'énoncé. On peut aussi écrire cela comme une inégalité: 62 < N < 104
Maintenant, nous savons que si on regroupe les N oeufs par paquets de 10, il nous en restera 5 à la fin.
Cela signifie que N-5 est un multiple de 10 (on peut diviser N-5 par 10).
Aussi, le nombre (N-5)/10 est égal au nombre de paquets de 10 formés.
Donc en prenant l'inégalité:
62<N<104
On retranche 5 aux trois membres:
(62-5)<N-5<104-5
Donc 57<N-5<99
En divisant par 10 les trois membres:
5.7<(N-5)/10 < 9.9
Le nombre de paquets de 10 est donc entre 6 et 9...
Si on a 6 paquets de 10, on aurait: 6*10+5=65 Billes
Si on a 7 paquets: 7*10+5=75 Billes
Si 8 paquets alors 85 billes
Si 9 on aurait 95 Billes.
Maintenant on doit refaire le même travail en regroupant les billes par paquets de 5.
De même (N-5)/5 va représenter le nombre de paquets de 5. Nous écrivons donc l'inégalité qui correspond:
62<N<104
Donc 57<(N-5)<99
11.4 < (N-5)/5 < 19.8
On a donc entre 12 et 19 paquets de 5.
Si on en a 12, on a donc 12*5+5=65 Billes
Si on en a 13 alors 70 Billes
Si on en a 14 alors 75 billes
Ainsi de suite...
On se rend compte des possibilités pour que le même nombre total de billes coïncide dans chaque cas.
65 billes convient par exemple.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Petit problème
Salut,
(comme je connais pas le programme de maths en Belgique je vous propose une solution qui marche bien)
On pose le nombre d’œufs qu'ils ont ramassé.
le nombre d’œufs qu'ils ont ramassé.
Les deux hypothèses de l'énoncé nous donne :
il existe un entier tels que
tels que 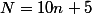 (1)
(1)
il existe un entier tels que
tels que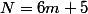 (2)
(2)
Donc on a
Comme 5 et 3 sont premiers entre eux on a forcément que 3 divise n et que 5 divise m (ça c'est d'après Gauss mais bon votre fille ne l'a peut-être pas vu)
Or comme :
:
(*) On a d'après (1) :
Mais comme 3 divise n alors forcément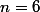 ou
ou 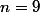 .
.
Donc ou
ou 
(*) On a aussi d'après (2) :
Mais comme 5 divise m alors forcément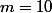 ou
ou 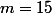
Donc ou
ou 
Conclusion : Ils ont ramassé 65 ou 95 œufs.
[Edit : j'étais entrain d'écrire en même temps que Lostounet l'idée est la même mais en utilisant Gauss on a pas besoin de faire de tâtonnement]
(comme je connais pas le programme de maths en Belgique je vous propose une solution qui marche bien)
On pose
Les deux hypothèses de l'énoncé nous donne :
il existe un entier
il existe un entier
Donc on a
Comme 5 et 3 sont premiers entre eux on a forcément que 3 divise n et que 5 divise m (ça c'est d'après Gauss mais bon votre fille ne l'a peut-être pas vu)
Or comme
(*) On a d'après (1) :
Mais comme 3 divise n alors forcément
Donc
(*) On a aussi d'après (2) :
Mais comme 5 divise m alors forcément
Donc
Conclusion : Ils ont ramassé 65 ou 95 œufs.
[Edit : j'étais entrain d'écrire en même temps que Lostounet l'idée est la même mais en utilisant Gauss on a pas besoin de faire de tâtonnement]
Re: Petit problème
Merci à vous 2 pour les réponses.
Elle n'a effectivement pas vu Gauss et je pense que si je tente de lui expliquer votre méthode, je vais la perdre
Dommage car en effet cela évite le tâtonnement.
Je vais lui expliquer la méthode précédente.
Merci !!
Elle n'a effectivement pas vu Gauss et je pense que si je tente de lui expliquer votre méthode, je vais la perdre
Dommage car en effet cela évite le tâtonnement.
Je vais lui expliquer la méthode précédente.
Merci !!
Re: Petit problème
Salut,
A mon avis, vu les valeur de l'énoncé, en particulier l'intervalle des possibilités qui n'est "pas très grand", un truc qui risque d'être attendu, ça pourrait être simplement :
1) Le nombre d’œuf, c'est un certain nombre de "paquet de 10" plus 5, donc il se termine par 5 (écrit en base 10 bien sûr) : Vu le bornes données par l'énoncé, c'est donc 65 ou 75 ou 85 ou 95.
2) On regarde pour chacun de ces 4 nombres si le reste de la division par 6 donne 5 ou pas :
65=6x10+5-> OK ; 75=6x12+3->NON ; 85=6x14+1->NON ; 95=6x15+5->OK
En procédant de la sorte, en terme de "longueur de la preuve", c'est pas plus long que les trucs "plus théorique" proposés précédemment. Bien sûr, si elle arrive à comprendre un raisonnement "plus subtil", alors tant mieux, mais c'est peut être pas bête de signaler que, vu la "petitesse" de l'intervalle donné au départ, faire dans le "plus subtil" n'est pas indispensable ici (et c'est toujours pas con d'expliquer qu'il y a plusieurs méthodes pour répondre à une même question)
A mon avis, vu les valeur de l'énoncé, en particulier l'intervalle des possibilités qui n'est "pas très grand", un truc qui risque d'être attendu, ça pourrait être simplement :
1) Le nombre d’œuf, c'est un certain nombre de "paquet de 10" plus 5, donc il se termine par 5 (écrit en base 10 bien sûr) : Vu le bornes données par l'énoncé, c'est donc 65 ou 75 ou 85 ou 95.
2) On regarde pour chacun de ces 4 nombres si le reste de la division par 6 donne 5 ou pas :
65=6x10+5-> OK ; 75=6x12+3->NON ; 85=6x14+1->NON ; 95=6x15+5->OK
En procédant de la sorte, en terme de "longueur de la preuve", c'est pas plus long que les trucs "plus théorique" proposés précédemment. Bien sûr, si elle arrive à comprendre un raisonnement "plus subtil", alors tant mieux, mais c'est peut être pas bête de signaler que, vu la "petitesse" de l'intervalle donné au départ, faire dans le "plus subtil" n'est pas indispensable ici (et c'est toujours pas con d'expliquer qu'il y a plusieurs méthodes pour répondre à une même question)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Petit problème
Bonjour,
Oui je vais lui expliquer cette Méthode aussi.
Elle est peut être plus de son niveau.
Merci !
Oui je vais lui expliquer cette Méthode aussi.
Elle est peut être plus de son niveau.
Merci !
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
