Numération à 3 Inconnus

[Shorrion]

[CENTER]Bonjour à toutes et à tous !
J'ai un léger problème qui me tracasse depuis peu, je n'arrive pas a m'en défaire et y trouver la solution.
Il faut que dans le chiffre "220 012" je trouve combien de fois il y a les chiffre "11, 7 et 5".
Donc j'avais pensé a ça :

(11 x a ) + (7 x b) + (5 x c) = 220 012

ou bien

a + b + c = n

Est-ce vraiment comme ça qu'il faut trouvé si oui je ne sais plus comment faire.
J'aimerai être éclairé car je m'en sors plus, merci. [/CENTER]

[nodjim]

Ta question est on ne peut plus ambiguë. Peux tu recopier exactement l'énoncé s'il te plait ?

[schwa]

Bonjour !

Tout d'abord petite précision, 220 012 est un nombre, pas un chiffre (c'est un peu comme si tu dis que "mot" est une lettre. Les chiffres servent à constituer des nombres. Il y a 10 chiffres en tout et une infinité de nombres).


Mais là n'est pas le problème !

Hmm. Alors peut-être est-ce quelque chose de plus compliqué attendu, mais moi je vois 22 qui st le double de 11, et 12=7+5.
Alors peut-être tout simplement 220 012 = 11x20 000 + 5 + 7 ?

[Lostounet]

Je crois qu'il veut résoudre l'équation 5x + 7y + 11z = 220012 avec x, y et z trois entiers.
Tu es en quelle classe ?

[schwa]

Dans ce cas, x=20 000 ; y=z=1 ?

[Lostounet]

Dans ce cas, x=20 000 ; y=z=1 ?

Pour z = 0, il y a par exemple tous les entiers (relatifs) de la forme:





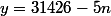
Pour n = 2, cela donne x = 20, y =31416, z = 0. C'est une équation diophantienne donc souvent elle admet une infinité de solutions... Après, je ne sais pas qu'est-ce qui se passe si on laisse les trois variables ..varier. (Pour deux je sais faire) :ptdr: :zen:

Pour chaque z, il y aura une infinité de solutions... Vu qu'on travaille dans un plan. pour chaque z, il y aurait une droite sur laquelle on doit repérer les points à coordonnées entières.