Montrer que 3x=5
Réponses à toutes vos questions du CP à la 3ème
-
MATH&ME
- Membre Relatif
- Messages: 340
- Enregistré le: 29 Nov 2011, 18:59
-
 par MATH&ME » 15 Juil 2012, 16:39
par MATH&ME » 15 Juil 2012, 16:39
Salut à tous .
Alors dans l'éxercice :
On veut détérminer l'abscisse du point

symbolisé par

dans un repére
 . OI=OJ)
1- En calculant de deux façons la surface du triangle

, montrer que
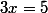
2-Quelle est la valeur approximative de l'abscisse de

.
3-qu'est ce qu'on peut déduire de ce qui précéde .
1- les deux méthodes de calcul :
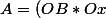/2)
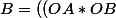/2)-((OA*Ex)/2))
Je ne sais pas comment justifier cette équation par rapport à la figure.
2-
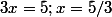
3- ?????


-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 15 Juil 2012, 23:15
par Lostounet » 15 Juil 2012, 23:15
Yo salut,
Soit H (0 ; 2).
L'aire du triangle OBE peut s'exprimer des deux façons suivantes:
*
Aire (OBE) = Aire (HEB) + Aire (HOE)
Aire (HEB) = HE * EB / 2 = x/2
Aire (HOE) = HE * HO/2 = 2x/2 = x
Et donc Aire (HEB) + Aire (HOE) = 3x/2
Aire (OBE) = 3x/2
Et la deuxième façon:
Aire (OBE) = Aire (OAB) - Aire (OAE)
= 7.5 - ....
On a donc Aire (OBE) = 3x/2
Et Aire (OBE) = ...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
MATH&ME
- Membre Relatif
- Messages: 340
- Enregistré le: 29 Nov 2011, 18:59
-
 par MATH&ME » 15 Juil 2012, 23:29
par MATH&ME » 15 Juil 2012, 23:29
Lostounet a écrit:Yo salut,
On a donc Aire (OBE) = 3x/2
Et Aire (OBE) = ...
Comment t'a mis 3x/2 = Aire(OBE) ?
C'est tellement vague pour moi.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 16 Juil 2012, 21:55
par Lostounet » 16 Juil 2012, 21:55
MATH&ME a écrit:Comment t'a mis 3x/2 = Aire(OBE) ?
C'est tellement vague pour moi.
Yi?
C'est tout simple:
L'aire de (OBE), c'est l'aire de (BHE) + l'aire de (HEO) avec H(0 ; 2). Tu vois bien?
J'ai exprimé l'aire de (BHE) en fonction de x, j'ai trouvé x/2 et j'ai exprimé l'aire de (HEO) en fonction de x, j'ai trouvé x.
Donc l'aire de (OBE) qui est (BHE) + (HEO) = x/2 + x = ...

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
MATH&ME
- Membre Relatif
- Messages: 340
- Enregistré le: 29 Nov 2011, 18:59
-
 par MATH&ME » 16 Juil 2012, 22:18
par MATH&ME » 16 Juil 2012, 22:18
Lostounet a écrit:Yi?
C'est tout simple:
L'aire de (OBE), c'est l'aire de (BHE) + l'aire de (HEO) avec H(0 ; 2). Tu vois bien?
J'ai exprimé l'aire de (BHE) en fonction de x, j'ai trouvé x/2 et j'ai exprimé l'aire de (HEO) en fonction de x, j'ai trouvé x.
Donc l'aire de (OBE) qui est (BHE) + (HEO) = x/2 + x = ...

Comment t'a exprimé l'aire de (BHE) en fonction de x et trouvé x/2
aussi l'aire de (HEO) en fonction de x, comment t'a trouvé x.
J'ai pas encore etudie les fonctions .

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 16 Juil 2012, 22:36
par Lostounet » 16 Juil 2012, 22:36
L'aire d'un triangle, c'est Base * hauteur/2.
La base et la hauteur sont les côtés de l'angle droit, si le triangle est rectangle. BHE et HEO sont rectangles en H.
Aire (BHE) = Base * hauteur /2 = BH * HE/2
BH fait 1, et HE fait x car c'est l'abscisse de E... et donc ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
MATH&ME
- Membre Relatif
- Messages: 340
- Enregistré le: 29 Nov 2011, 18:59
-
 par MATH&ME » 16 Juil 2012, 23:10
par MATH&ME » 16 Juil 2012, 23:10
Lostounet a écrit:L'aire d'un triangle, c'est Base * hauteur/2.
La base et la hauteur sont les côtés de l'angle droit, si le triangle est rectangle. BHE et HEO sont rectangles en H.
Aire (BHE) = Base * hauteur /2 = BH * HE/2
BH fait 1, et HE fait x car c'est l'abscisse de E... et donc ?
1x/2 = Aire (BHE)
2x/2 = Aire (HEO)
Aire (OBE) = x/2+x = 3x/2
Mais quel est le rapport avec : 3x=5 ????

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 16 Juil 2012, 23:20
par Lostounet » 16 Juil 2012, 23:20
Ok l'aire de (OBE) c'est 3x/2.
Ensuite, on va exprimer l'aire de (OBE) autrement.
Aire (OBE) = Aire (OBA) - Aire (OEA)
= OB*OA/2 - OA*h/2 (Ici, h désigne la longueur de la hauteur issue du point E)
Continue
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
MATH&ME
- Membre Relatif
- Messages: 340
- Enregistré le: 29 Nov 2011, 18:59
-
 par MATH&ME » 16 Juil 2012, 23:40
par MATH&ME » 16 Juil 2012, 23:40
A demain et merci infiniment loustounet .
Toujours au sauvtage .
Thanks .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités

