bonjour , quelqu'un pourrait il m'aider à solutionner ce pb de calcul d'aire ?
...en utilisant le papier millimétré tracé, donner une valeur approchée de l'aire de l'ovale sans utiliser de formule, en comptant les carreaux.
https://www.cjoint.com/c/HBgxmLaoFCw
merci.
Mesure d'une aire avec du papier millimètre
7 messages
- Page 1 sur 1
Re: mesure d'une aire avec du papier millimètre
Bonjour
Soit A l'aire de l'ovale.
Il faut compter les petits carreaux strictement à l'intérieur de l'ovale. Ce qui donnera une aire
Puis ajouter à cela les petits carreaux qui coupent l'ovale. Ce qui donnera une aire
On a ainsi un encadrement de A. Comme approximation on peut faire une interpolation linéaire i.e.)
On devrait t trouver
Soit A l'aire de l'ovale.
Il faut compter les petits carreaux strictement à l'intérieur de l'ovale. Ce qui donnera une aire
Puis ajouter à cela les petits carreaux qui coupent l'ovale. Ce qui donnera une aire
On a ainsi un encadrement de A. Comme approximation on peut faire une interpolation linéaire i.e
On devrait t trouver
Re: mesure d'une aire avec du papier millimètre
Salut
On peut conseiller de tracer les axes de symétrie et d'évaluer l'aire du quart de l'ovale avant de multiplier par 4.
On peut conseiller de tracer les axes de symétrie et d'évaluer l'aire du quart de l'ovale avant de multiplier par 4.
Re: mesure d'une aire avec du papier millimètre
Oui Chan79, sauf que si tu comptes tout tu diminues l'erreur relative.
Re: mesure d'une aire avec du papier millimètre
donc pour vous aviateur , le résultat de ma figure est 17,53 cm2?
Re: mesure d'une aire avec du papier millimètre
L' aire d' une ellipse est 1/4 * pi * D x d. On a D = 62 mm et d = 35 mm, donc
aire A = 1/4 * pi* 62 * 35
aire A = 1704 mm2
Ou A = 17.04 cm2, si tu préfères.
Mais là, je triche un peu : on te demande de compter les petits carrés, le résultat que je te donne te sert juste à vérifier
aire A = 1/4 * pi* 62 * 35
aire A = 1704 mm2
Ou A = 17.04 cm2, si tu préfères.
Mais là, je triche un peu : on te demande de compter les petits carrés, le résultat que je te donne te sert juste à vérifier
Re: mesure d'une aire avec du papier millimètre
Bonjour
évidemment je ne me suis pas amusé à calculer les petits carreaux mais c'est ce qui est demandé de faire.
Par contre l'ovale ressemble à une ellipse et l'aire d'une ellipse c'est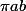
a et b étant = à la moitiés des axes. J'ai mesuré (à peu près les longueurs des axes et le A=17.53 cm^2 vient de ce calcul.
donc pour vous aviateur , le résultat de ma figure est 17,53 cm2?
évidemment je ne me suis pas amusé à calculer les petits carreaux mais c'est ce qui est demandé de faire.
Par contre l'ovale ressemble à une ellipse et l'aire d'une ellipse c'est
a et b étant = à la moitiés des axes. J'ai mesuré (à peu près les longueurs des axes et le A=17.53 cm^2 vient de ce calcul.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
