Mesure de l'angle dont on connait son sin et cos

[beka]

Salut
J'ai une question : Si la valeur de cos a = -3/5 et sin a = -4/5 alors que vaut la mesure de l'angle en radian ? ; j'utilise la calculatrice ( cos ^-1 et sin^-1) j'obtient deux valeurs différentes .

[Mateo_13]

Bonjour,

Salut
J'ai une question : Si la valeur de cos a = -3/5 et sin a = -4/5 alors que vaut la mesure de l'angle en radian ? ; j'utilise la calculatrice ( cos ^-1 et sin^-1) j'obtient deux valeurs différentes .

Avec ces deux valeurs on a bien donc ces deux valeurs sont cohérentes.

Si tu enlèves les deux signes "-" et que tu fais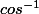 et 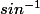, qu'obtiens-tu ?

Sur un cercle trigonométrique, que se passe-t-il pour l'angle lorsque son sinus et son cosinus deviennent leurs opposés ?

Cordialement,
--
Mateo.

[beka]

Dans ce cas j'obtient a= 0.92 mais a appartient à [-pi ; -pi /2 ] alors a = pi -0.92 ; C'est ça ou pas ?
Merci pour la réponse

[beka]

Bonjour,

Salut
J'ai une question : Si la valeur de cos a = -3/5 et sin a = -4/5 alors que vaut la mesure de l'angle en radian ? ; j'utilise la calculatrice ( cos ^-1 et sin^-1) j'obtient deux valeurs différentes .

Avec ces deux valeurs on a bien donc ces deux valeurs sont cohérentes.

Si tu enlèves les deux signes "-" et que tu fais et , qu'obtiens-tu ?

Sur un cercle trigonométrique, que se passe-t-il pour l'angle lorsque son sinus et son cosinus deviennent leurs opposés ?

Cordialement,
--
Mateo.

merci ca m'a aidé ; vous voulez dire que cos (pi + a ) = 3/5 donc a= cos^-1(3/5) - pi ??

[Mateo_13]

Je crois que tu as compris l'idée.

Fais un dessin de cercle trigonométrique pour vérifier tes résultats.

Cordialement,
--
Mateo.

[mathelot]

Bonjour,
quand cos() <0,arccos() renvoie un arc dans et quand sin() <0,arcsin() renvoie un arc dans .or il se trouve que la solution appartient à l'intervalle
On détermine dans tel que et ,la solution est alors soit 4.06889

[Black Jack]

Salut,

La réponse ayant été donnée ... en voici une variante.

cos(a) < 0 et sin(a) < 0 ---> a est dans le 3 eme quadrant, donc a dans ]-Pi ; -Pi/2[ (mod 2Pi)

arcos(-3/5) = 2,214297... rad

Se rappeler que cos(a) = cos(-a) --->

cos(a) = -3/5 --> a = 2,214297... rad ou a = -2,214297... rad.

C'est a = -2,214297... rad qui convient car compris dans ]-Pi ; -Pi/2[