Inverser un nombre

par **Eklips** » 04 Sep 2006, 16:45

L'énoncé que je vous ait donné au début est celui q'il m'a été donné:
Trouver une formule mathématique qui permet d'inverser n'importe quel nombre compris entre 1000 et 9999.

Je fait ce travail dans un cours d'initiation a la programmation en java et tout ce que j'ai appris pour le moment c'est les oppérations simples...alors je devrais être capable de trouver une réponse en n'utilisat que les signes de base (+-*/)

Votre formule c'est bien...mais j'arriverai jamais a la faire calculer avec mes quelques connaissances de java!

Merci de toutes les neurones que vous me consacrez!!

par **Oumzil** » 04 Sep 2006, 16:46

sollution en bref:
soit abcd le nombre que tu veux inverser :
abcd = a*1000 + b*100+ c*10 + d

alors en inversant les chiffres les actions qu'on fait sont :
1/diviser par 1000 le chiffres des milliers a
2/diviser par 10 le chiffre des centaine b
3/ multiplier par 10 le chiffre des dizaine c
4/ multiplier par 1000 le chiffre des unités

alors on doit considerer les 4 fonctions suivantes :
g(X) = X/1000 et h(X) = X/10 et p(X)= 10*X et q(X) = 1000*X

alors la formule que tu cherche est une fonction f(a,b,c,d) pour 4 nombre :
f(a*1000,b*100,c*10,d) = g(a) + h(b) + p(c) + q(d)

exemple :
inverser le nombre 1234
on a : f(1000,200,30,4) = 1 + 20 + 300 + 4000
= 4321

tu as compris cette sollution ?

par **Flodelarab** » 04 Sep 2006, 16:47

YES!

Merci pour cette consecration !

c exactement ce que je pensais! Mon argument de la division entière marche alors a 100% !!!!

ps: pkoi tu postes ton message dans "college" alors ?

par **nox** » 04 Sep 2006, 16:47

Donc mon cher eklips :

2 façon de voir le probleme

1) si on connait uniquement le nombre x, sans connaitre sa décomposition (1234 = 1000 + 200 + 30 + 4), on doit trouver une fonction de x qui inverse les chiffres de x.

dans ce cas la solution est :

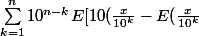ou

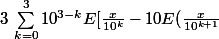c'est le cas général

2) si tu connais la décomposition, c'est à dire que tu connais le chiffre des unités, le chiffre des dizaines etc... alors c'est plus simple et la solution d'oumzil suffit :

tu veux inverser les nombre qui sont entre 1000 et 9999 , voilà une idée mais je ne sais pas si la sollution que tu cherches :

on sait que : tout les nombre en tre 1000 et 9999 sont composés de 4 chiffres
alors : chaque X de ces nombres est écrit de la forme : 1000*a+100*b+10*c+d ( ou a , b ,c et d sont des entiers )
alors : en inversant les nombres on obtient le nombre suivant : 1000*d+100*c+10*c+a

alors en inversant les chiffres les actions qu'on fait sont :
1/diviser par 1000 le chiffres des milliers a
2/diviser par 10 le chiffre des centaine b
3/ multiplier par 10 le chiffre des dizaine c
4/ multiplier par 1000 le chiffre des unités

alors on doit considerer les 4 fonctions suivantes :
g(X) = X/1000 et h(X) = X/10 et p(X)= 10*X et q(X) = 1000*X

alors la formule que tu cherche est une fonction f(a,b,c,d) pour 4 nombre :
f(a*1000,b*100,c*10,d) = g(a) + h(b) + p(c) + q(d)

exemple :
inverser le nombre 1234
on a : f(1000,200,30,4) = 1 + 20 + 300 + 4000
= 4321

par **Oumzil** » 04 Sep 2006, 16:48

c'est bon pour inverser ces nombre tu as 4 actions à effectuer :
1/diviser par 1000 le chiffres des milliers a
2/diviser par 10 le chiffre des centaine b
3/ multiplier par 10 le chiffre des dizaine c
4/ multiplier par 1000 le chiffre des unités

par **nox** » 04 Sep 2006, 16:48

ah oui je crois que pour la programmation notre solution s'impose...c'est même précisément à ce genre de cas que je pensais :happy2:

donc la formule est :

ou

par **Flodelarab** » 04 Sep 2006, 16:49

tu penses a l'info et tu fais des divisions de nombres a virgules ?

Je ne te félicite pas

par **Oumzil** » 04 Sep 2006, 16:51

au cas ou cas ou tu veux utiliser ces 4action utilise 4 formulaire un pour les unité , un pour les dizaines ,un pour les centaines et un pour les milliers
et effectue les 4 actions

par **nox** » 04 Sep 2006, 16:51

plait il ???

ba qu'est ce qui t'embete dans ma formule pour l'info?

PS : c'est le bordel ce topic nan?

par **Oumzil** » 04 Sep 2006, 16:52

eklips t'as trouvé parmis les sollution celle que tu veux ? sinon décrit un petit peu plus

par **Flodelarab** » 04 Sep 2006, 16:52

Oumzil a écrit:au cas ou cas ou tu veux utiliser ces 4action utilise 4 formulaire un pour les unité , un pour les dizaines ,un pour les centaines et un pour les milliers
et effectue les 4 actions

l'Utilisateur se sera barré avant le 4eme formulaire :-)

par **nox** » 04 Sep 2006, 16:53

:ptdr: :ptdr: :ptdr: :ptdr: :ptdr:

par **Oumzil** » 04 Sep 2006, 16:54

non mais un formulaire dans la programation cune petite surface pour enter les donnés bon peut avoir meme 1 cm² de surface pour chaque chiffre ac un bouton valider

par **nox** » 04 Sep 2006, 16:55

wai donc tu pars du principe que t'as une GUI (interface graphique)

la je pense que non quand même...

par **Oumzil** » 04 Sep 2006, 16:56

fini pour ce sujet je crois non ?

par **nox** » 04 Sep 2006, 16:56

wai depuis longtemps...dans les 3 premiers posts on avait tout...mais on rigole fort

PS : 3 premiers posts -> le mien, celui d'Oumzil et celui de Flodelarab évidemment

par **Oumzil** » 04 Sep 2006, 16:58

nox ya pas de GUI lé totalement modifiable , bon il s'agit de language JAVA bon jconnais pas trop pour le java mais pour PHP / HTML /SQL c'est très facile à faire et jpeux meme programer celà si vous voulez voir

par **Oumzil** » 04 Sep 2006, 16:59

oui ca serai pas très possible au cas ou ya des modérateurs

par **Eklips** » 04 Sep 2006, 17:00

Mais ce n'est pas tout a fait ce que je cherche!!!!
Vos deux solutions se tiennent mais je ne vois pas comment je pourrais séparer les unitées des dizaines des centaines des milliers...tout ce que je peux utiliser c'est /*-+ prendre les unitées ou les dizaines tout seul je ne peux pas....

par **nox** » 04 Sep 2006, 17:01

ba oui on peut toujours programmer...en programmation on peut tout faire...

mais je pense que la pour une initiation c'est pas trop ca...et informatiquement notre méthode à Flodelarab et moi est tout de même plus simple je crois...

Inverser un nombre

l'énoncé générale

fin

Désolé

Qui est en ligne