Hauteur d'une pyramide de boules à base carré

[Dlzlogic]

Bravo,
Si tu commences par une seule boule bleue, puis les triplets orange - bleu etc, tu termines pareil, mais tu gagnes 2 boules. Tu me répondras, "bof, ça mais même pas 1%".
En tout cas, bravo, moi j'avais pas trouvé.

[LeJeu]

Bravo,
Si tu commences par une seule boule bleue, puis les triplets orange - bleu etc, tu termines pareil, mais tu gagnes 2 boules. Tu me répondras, "bof, ça mais même pas 1%".
En tout cas, bravo, moi j'avais pas trouvé.

Mais oui bien sûr !
la serie de distance est maintenant d /d / 2

1 + 6x -> L = R ( 1 +x (d+d+2) +1)
à comparer avec R *6x

on a toujours

pour x = 55 soit 331 boules, L = 330,0166486 à comparer à 330 : presque!
on continue

mais pour le suivant on rajoure d maintenant et non 2
p our x = 55 +2boules soit 333 boules L = 331,9986182à comparer à 332

Ca ferme !

[Dlzlogic]

Tout le monde a compris ?

[fma]

Tout le monde a compris ?

Non, je suis perplexe.
Les schémas sont faux car s'ils étaient exacts, les 6 boules en bas du 2ème dessin seraient tangentes à la base du coffre rectangulaire et aux boules adjacentes.
Donc "visiblement" on ne peut pas s'appuyer sur une géométrie dont les cotes sont incertaines.
Rappel : Un coffre dont l'intérieur, en forme de parallélépipède, a pour largeur 2d, pour longueur nd et pour hauteur d.

[LeJeu]

Non, je suis perplexe.
Les schémas sont faux car s'ils étaient exacts, les 6 boules en bas du 2ème dessin seraient tangentes à la base de coffre rectangulaire et aux boules adjacentes.
Donc "visiblement" on ne peut pas s'appuyer sur une géométrie dont les cotes sont incertaines.

Salut,

C'est justement l'idée, de ne pas avoir les boules tangentes au bas du coffre, mais d'organiser un quinconce qui permet d'avoir des intervalles de 1,9 au lieu de deux

Evidemment on perd un boule dès le départ : 12 en haut , et 11 en bas, mais en mettant suffisamment de séries 1,9 - 1,9 - 2 on rattrape notre retard , grosso modo apres 150 boules, et on prend une boule d'avance avec 333

[fma]

Salut,

C'est justement l'idée, de ne pas avoir les boules tangentes au bas du coffre, mais d'organiser un quinconce qui permet d'avoir des intervalles de 1,9 au lieu de deux

Evidemment on perd un boule dès le départ : 12 en haut , et 11 en bas, mais en mettant suffisamment de séries 1,9 - 1,9 - 2 on rattrape notre retard , grosso modo apres 150 boules, et on prend une boule d'avance avec 333

Ok, mais dans ces 2 coffres équivalents, cette configuration est impossible, si je m'en réfère aux schémas.
Pour raisonner avec efficacité il faudrait un dessin avec géogébra

[fma]

Voilà le premier dessin, peux-tu faire le deuxième avec les boules en quinconces

[chan79]

salut
je n'ai pas regardé les calculs mais le dessin pourrait être ça

[fma]

Y en a qui sont plus rapide que la lumière pour faire un beau dessin !
Les cotes qui semblent exactes à vue d'oeil (en fait oui/non ?) montrent au moins que ce qui reste de la septième boule en bas à droite, devrait remplir l'espace en bas à gauche et même moins si on veut plus loin en mettre une de plus.
Si ce raisonnement est juste, est-ce le cas ?

En quelque sorte que ce reste W de la boule ne remplisse, par exemple, pas plus d'espace que celui offert par W' pour gagner un peu sur les 7d (des 7 boules)

[LeJeu]

Y en a qui sont plus rapide que la lumière pour faire un beau dessin !
Les cotes qui semblent exactes à vue d'oeil (en fait oui/non ?) montrent au moins que ce qui reste de la septième boule en bas à droite, devrait remplir l'espace en bas à gauche et même moins si on veut plus loin en mettre une de plus.
Si ce raisonnement est juste, est-ce le cas ?

En quelque sorte que ce reste W de la boule ne remplisse, par exemple, pas plus d'espace que celui offert par W' pour gagner un peu sur les 7d (des 7 boules)

Salut

Ce n'est pas tellement les espaces W et W' qui sont importants
mais le fait que la distance horizontale entre deux boules bleues et rouges tangentes soit plus petire que dans le rangement initial ( 1,98 par rapport à 2) et que, plus tu mets de boules plus tu gagnes de places

sur Le dessin de Chan le calcul de la longueur en partant du bord gauche donne ( somme des distances horizontales entre les centres)
1 + ( d+2+d) +(d+2+d)......

on peu tasser un peu plus en retirant la première boule pour trouver
1 +( d+d+2) +(d+d+2)

bien sur tous les 3 billes on retombe sur la même distance

c'est la figure que proposait Dzlogic

[chan79]

Salut
D'accord avec LeJeu et Dlzlogic.

En prenant 1 pour le rayon des boules
AB=2+2d+2 (avec un groupe rouge entre A et B)
AC=2+(2d+2)+(2d+2) (avec deux groupes rouges entre A et C)
AD=2+3(2d+2) (avec trois groupes rouges entre A et D)
Avec par exemple 1000 groupes rouges, on a la distance 2+1000(2d+2).
En ajoutant 1 à chaque bout, on voit que ces 6003 boules (3000 rouges et 3003 bleues) logent dans une boîte de longueur 2000d+2004 soit environ 5967,93
Dans une boîte de longueur 5968, on peut donc en loger 6003 alors qu'avec l'autre disposition, on ne pourrait en loger que 5968. On gagne bien de la place.
Avec la disposition ci-dessus, le taux de remplissage tend vers soit 0,7901... contre soit 0,7853... pour l'autre disposition
A comparer avec la densité du meilleur arrangement de disques dans le plan,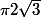 soit 0.906899... avec les centres qui forment un réseau triangulaire

Avec la disposition ci-dessous, et avec n groupes rouges (sans compter la rouge isolée de gauche), la longueur nécessaire est 2+ d + n(2d+2) et le nombre de boules est 6n+3
on trouve que pour n=55 soit 333 boules, la longueur nécessaire est 331,9986182... ce qui confirme les calculs de LeJeu (comme d'habitude :zen: )

[fma]

Salut
D'accord avec LeJeu et Dlzlogic.

En prenant 1 pour le rayon des boules
AB=2+2d+2 (avec un groupe rouge entre A et B)
AC=2+(2d+2)+(2d+2) (avec deux groupes rouges entre A et C)
AD=2+3(2d+2) (avec trois groupes rouges entre A et D)
Avec par exemple 1000 groupes rouges, on a la distance 2+1000(2d+2).
En ajoutant 1 à chaque bout, on voit que ces 6003 boules (3000 rouges et 3003 bleues) logent dans une boîte de longueur 2000d+2004 soit environ 5967,93
Dans une boîte de longueur 5968, on peut donc en loger 6003 alors qu'avec l'autre disposition, on ne pourrait en loger que 5968. On gagne bien de la place.
Avec la disposition ci-dessus, le taux de remplissage tend vers soit 0,7901... contre soit 0,7853... pour l'autre disposition
A comparer avec la densité du meilleur arrangement de disques dans le plan, soit 0.906899... avec les centres qui forment un réseau triangulaire

Oui, là c'est clair, merci
Dans le cas présent, l'intuition est mise à mal par la quantité d'objets qu'on a pas l'habitude de manipuler. Sans calcul (maintenant qu'on a la solution) on se rend compte qu'il était possible de préméditer la bonne conclusion.
Bien joué

[Dlzlogic]

Bonjour,
Un problème un peu comparable a été posé sur un autre forum :
http://forums.futura-sciences.com/mathematiques-superieur/604087-nombre-de-petits-hexagones-un-grand-hexagone-2.html
Apparemment il s'agit d'un problème réel, mais malheureusement les hypothèses sont fausses ou imprécises.
Par contre, j'ai essayé de faire une évaluation du nombre de cylindres. Je crois que le problème mérite qu'on s'y penche 5 mn.

[chan79]

Bonjour,
Un problème un peu comparable a été posé sur un autre forum :
http://forums.futura-sciences.com/mathematiques-superieur/604087-nombre-de-petits-hexagones-un-grand-hexagone-2.html
Apparemment il s'agit d'un problème réel, mais malheureusement les hypothèses sont fausses ou imprécises.
Par contre, j'ai essayé de faire une évaluation du nombre de cylindres. Je crois que le problème mérite qu'on s'y penche 5 mn.

Salut Dlzlogic
Ce n'est sans doute pas la réponse attendue mais du point de vue mathématique, en dénombrant les disques de rayon 1 inclus dans le disque de rayon 47,28 on arrive, avec cette disposition des disques, à 1945.
Les disques de l'hexagone sont faciles à compter. Il faut rajouter 6 fois 28 (second dessin).
Avec geogebra, pour gagner du temps, il faut utiliser la commande Séquence.

[Dlzlogic]

Bonjour Chan,
Donc, j'étais largement en-dessous de la bonne valeur. Je vais essayer de trouver où je me suis trompé.

[leon1789]

chan79 nous gratifie d'un festival de beaux dessins ! :++:

[Dlzlogic]

@ Chan79
J'ai revu mes calculs.
Mais il me semble que ton calcul est un calcul exact.
L'approche que j'ai essayé de faire est basée sur le principe que le "coefficient d'occupation" est V3/2 ~0.866025
Soit 1935 petits cercles (je m'étais trompé dans mes calculs).
Puis j'essayais de trouver une borne maxi et une borne mini en faisant intervenir la longueur du périmètre.
Donc, dans le cas présent, il semble qu'on peut en rajouter 10 de plus que la moyenne.

[chan79]

@ Chan79
J'ai revu mes calculs.
Mais il me semble que ton calcul est un calcul exact.
L'approche que j'ai essayé de faire est basée sur le principe que le "coefficient d'occupation" est V3/2 ~0.866025
Soit 1935 petits cercles (je m'étais trompé dans mes calculs).
Puis j'essayais de trouver une borne maxi et une borne mini en faisant intervenir la longueur du périmètre.
Donc, dans le cas présent, il semble qu'on peut en rajouter 10 de plus que la moyenne.

Avec la disposition ci-dessus, on arrive à un taux de remplissage de 0.87009...
J'ai du mal à imaginer un autre agencement plus compact mais il existe peut-être ...
A part ça, d'où vient le nombre 4728 ?

[Dlzlogic]

Plus compact, je ne pense vraiment pas, je dirais même que suivant mon calcul d'approximation en utilisant le périmètre, j'arrive à plus ou moins 5, et c'est justement cette partie là du calcul qui m'intéresse. En d'autres termes je cherche une généralisation du problème.
Le nombre 47.28 vient des hypothèses de base, mais en l'occurrence, ce n'est dans mon esprit que l'application numérique. On pourrait dire aussi, le diamètre du grand cercle est environ 50 fois plus grand que celui des petits cercles.
On sait que le coef d'occupation (moyen) est 0.866025, dans tous les cas, connaissant le rapport des rayons, on en déduit directement le nombre "moyen" de petits cercles. Ce nombre est bon dans quelles limites ? On ne dispose pas de géogebra, et il s'agit juste d'un calcul théorique.

[LeJeu]

Avec la disposition ci-dessus, on arrive à un taux de remplissage de 0.87009...
J'ai du mal à imaginer un autre agencement plus compact mais il du ste peut-être ...
A part ça, d'où vient le nombre 4728 ?

Salut,

En reprenant dans le bons sens l'idée de Dzlogic d'un post précédent

Il me semble que l'on peut estimer le nombre de billes en fonction du rayon R , du taux de remplissage théorique rappelé par Chan : soit 0.906899... , et d'une modélisation de l'effet de bord

En fait sur le bord du grand cercle il y a une bande non remplie qui a pour largeur en moyenne une demi diamètre de petit cercle

Donc on peut estimer le nombre de billes comme ( R-1)² *

avec 47,28 on trouve un nombre de billes de 1942,43 ce qui est pas mal au vu du résultat de chan

Bien sûr plus le R augmente plus on va converger vers le rapport théorique