Fractions et puissances 3ème
14 messages
- Page 1 sur 1
Fractions et puissances 3ème
Salut à tous et à toutes!
Mon prof de math vient de nous donner un gros DM pour la semaine prochaine, sur ce que l'on va faire cette année.
Donc on est prit un peu au dépourvut!
Ce DM ne comptera normalement pas pour la moyenne mais je préfererais quand même le réussir.
Je viens donc vous demander votre aide et vos explications SVP.
EXERCICE 1 : calculer
D =
3- (2sur5) + (4sur3)
divisé par :
2 + (4sur5) - (2sur3)
E =
5(puissance 4) x 5 (puissance -17)
divisé par
(5puissance de -5) x puissance de 3
Exercice 2 : Simplifier :
F =
(a puissance 2) x puissance 4 x a(puissance -7)
G =
8a(puissance -2)b
divisé par :
(2a-puissance 2- b) puissance 3
Alors j'ai bien conscience que ma présentation n'est pas très claire, et je m'en excuse, mais j'ai essayé de faire le plus simple possible, et normalement c'est compréhensible.
Merci d'avance les amis, et franchement je trouve que ce forum est une vraie bénédiction, donc continuez!! :++:
Mon prof de math vient de nous donner un gros DM pour la semaine prochaine, sur ce que l'on va faire cette année.
Donc on est prit un peu au dépourvut!
Ce DM ne comptera normalement pas pour la moyenne mais je préfererais quand même le réussir.
Je viens donc vous demander votre aide et vos explications SVP.
EXERCICE 1 : calculer
D =
3- (2sur5) + (4sur3)
divisé par :
2 + (4sur5) - (2sur3)
E =
5(puissance 4) x 5 (puissance -17)
divisé par
(5puissance de -5) x puissance de 3
Exercice 2 : Simplifier :
F =
(a puissance 2) x puissance 4 x a(puissance -7)
G =
8a(puissance -2)b
divisé par :
(2a-puissance 2- b) puissance 3
Alors j'ai bien conscience que ma présentation n'est pas très claire, et je m'en excuse, mais j'ai essayé de faire le plus simple possible, et normalement c'est compréhensible.
Merci d'avance les amis, et franchement je trouve que ce forum est une vraie bénédiction, donc continuez!! :++:
salut!
alors pour le premier exercie, il faut que tu simplifies le nominateur et le denominateur.
D= [ 3 - (2/5) + (4/3) ] / [ 2 + (4/5) - (2/3)]
on simplifie le nominateur:
3 - (2/5) + (4/3) = (3*15) - (6/15) + (20/15) = 59/15
on simplifie le denominateur:
2 + (4/5) - (2/3) = (2*15) + (12/15) + (10/15) = 52/15
ca donne donc (59/15) / (52/15). sachant que c'est une division de 2 fraction, tu vas multiplier (59/15) par l'inverse de (52/15), c'est à dire (15/52) .
ensuite tu supprimes 15 au nominateur et au denominateur et tu as la reponse.
(je sais pas trop si j'ai été clire ou pas. si besoin, redemande)
alors pour le premier exercie, il faut que tu simplifies le nominateur et le denominateur.
D= [ 3 - (2/5) + (4/3) ] / [ 2 + (4/5) - (2/3)]
on simplifie le nominateur:
3 - (2/5) + (4/3) = (3*15) - (6/15) + (20/15) = 59/15
on simplifie le denominateur:
2 + (4/5) - (2/3) = (2*15) + (12/15) + (10/15) = 52/15
ca donne donc (59/15) / (52/15). sachant que c'est une division de 2 fraction, tu vas multiplier (59/15) par l'inverse de (52/15), c'est à dire (15/52) .
ensuite tu supprimes 15 au nominateur et au denominateur et tu as la reponse.
(je sais pas trop si j'ai été clire ou pas. si besoin, redemande)
Re,
donc on a:
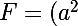^4\times{a^{-7}})
on utilises ds 1 premier temps^p=a^{n\times{p}})
donc
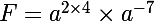
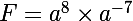
ensuite on utilise
donc
 donc F=a
donc F=a
pour G c'est donc
^2\times{b}}{(2a^{-2}\times{b})^3})
il faut dejà utiliser une des 2 propriétés ennoncées ci-dessus et en plus utiliser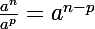
essaies de le faire dis ce que tu trouves et on te dira si c'est bon ou pas
Alors pour le F non il ne manque aucun a c'est bien comme je l'ai écrit
entre parenthèses : a puissance 2 le tout puissance 4 fois a puissance -7.
Et pour le G c'est ça sauf qu'il n'y a pas de moins dans la partie basse de la division (entre 2a puissance 2 et b)
donc on a:
on utilises ds 1 premier temps
donc
ensuite on utilise
donc
pour G c'est donc
il faut dejà utiliser une des 2 propriétés ennoncées ci-dessus et en plus utiliser
essaies de le faire dis ce que tu trouves et on te dira si c'est bon ou pas
fonfon a écrit:Re,
donc on a:
on utilises ds 1 premier temps
donc
ensuite on utilise
doncdonc F=a
pour G c'est donc
il faut dejà utiliser une des 2 propriétés ennoncées ci-dessus et en plus utiliser
essaies de le faire dis ce que tu trouves et on te dira si c'est bon ou pas
Merci pour le F!
Par contre je n'ai vraiment pas réussi le G. Enfin dit toi que je n'ai jamais fait ça avant, même avec tes (bonnes) explications je n'y arrive pas
fonfon a écrit:Salut,
essaies de regarder ce que j'ai fait avec les propriété que j'avais ennoncé si tu as un pb fais signe
Sincèrement merci pour ton aide fonfon.
J'ai étudié ta réponse. J'ai compris ton raisonnement mais je n'ai pas compris le pourquoi :
-Lors de la 4ème étape, je n'ai pas compris pourquoi tu as tout "mélangé" :hein:
-Pourquoi avoir réécrit le calcul en fraction lors de la dernière étape?
:++:
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
