Fraction irréductible.

[Anonyme]

Bonjour, je voudrais savoir comment peut-on reconnaître une fraction irréductible sans utiler de PGCD.
Merci bien.

[Nightmare]

Tu décompose le numérateur et le dénominateur en produit de facteurs premiers

:happy3:
Jord

[Alpha]

Salut,

Par définition, une fraction irréductible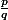 est une fraction dont on ne peut peut simplifier aucun des facteurs du numérateur et du dénominateur entre eux, ce qui est le cas si et seulement si p et q n'ont pas de diviseur commun supérieur ou égal à 2, c'est-à-dire ssi p et q sont premiers entre eux, soit donc .

C'est la définition d'une fraction irréductible.

:happy3:

[julian]

Sacré Alpha! :ptdr:
Je ne suis aps sûr que j'aurai pu comprendre çà lorsque j'étais encore au collège! :marteau: :ptdr:

[cesar]

bonjour,
je vous propose le truc suivant (c'est parfois un peu long, mais cela marche à tous les coups...).
soit P/q une fraction. on prend le sup de p et q.
supposons que cela soit p (mais cela marche pareil avec q, si q est le sup....)
on divise

P = a0*q + r1

puis on fait :
q = a1*r1 + r2
r1=a2*r2 + r3
etc ... on divise chaque fois le reste r n-1 par le reste r n...
la suite des r n est positive et décroisante. Elle est donc minorée par 0 et fini donc par s'arréter à 0...(cette limite n'a rien d'évident, mais on peut demontrer que c'est celle là).
la propriéte : si le dernier r n non nul est 1 alors P est premier avec q.

autre propriété : le dernier reste non nul est le PGCD...