Formule général non comprise 3ème
17 messages
- Page 1 sur 1
Formule général non comprise 3ème
Bonjour je vien de revoir tout mon trimestre de math sur cette derniére semaine et je me rend conte qu'il y a quelque chose que je n'ai vrément pas compris :triste: je vais vous lire l'exercice que notre proffessuer nous a corriger avant les vacances( le a et le b dans la formule son enba a droite du x c'est cela que je ne comprend pa ce que ça signifie)
:Soit (xA(en bas),ya(en bas)) et (xb(en bas),yb(en bas) les coordoné de A et B.En réfléchissant aux calculs précedent, exprimer AB² en fonction de xA(en bas),xb(en bas),ya(en bas) et yb (en bas) en déduire:
le prof nous a di que c'était AB=(xb-xa)²+(yb-ya)(les a et b en bas)
donc voila je ne comprenp pas ce que signifie tout ça je toruve que sa ressemble a un exo de teminal S de surdoué mais bon :ptdr: si quelqun peut maider se serait vrément cool :happy2:
:Soit (xA(en bas),ya(en bas)) et (xb(en bas),yb(en bas) les coordoné de A et B.En réfléchissant aux calculs précedent, exprimer AB² en fonction de xA(en bas),xb(en bas),ya(en bas) et yb (en bas) en déduire:
le prof nous a di que c'était AB=(xb-xa)²+(yb-ya)(les a et b en bas)
donc voila je ne comprenp pas ce que signifie tout ça je toruve que sa ressemble a un exo de teminal S de surdoué mais bon :ptdr: si quelqun peut maider se serait vrément cool :happy2:
euh ...
Bonjour Ju1s,
je ne sais pas si c'est moi, mais tu as dû mal expliquer j'ai du mal à comprendre :hein:
Pourrais tu ré-éditer ton premier message avec un peu plus de mise en forme que je puiss mieux comprendre ton problème ?
Et mets la classe dans laquelle tu es dans le nom du topic s'il-te-plait :ptdr:
Je t'aiderai si je comprend :happy2:
je ne sais pas si c'est moi, mais tu as dû mal expliquer j'ai du mal à comprendre :hein:
Pourrais tu ré-éditer ton premier message avec un peu plus de mise en forme que je puiss mieux comprendre ton problème ?
Et mets la classe dans laquelle tu es dans le nom du topic s'il-te-plait :ptdr:
Je t'aiderai si je comprend :happy2:
Merci c'est très gentil alor je refait ( je suis en 3éme) ^^
Soit (xa,ya) et (xb,yb) les coordonnées de A et B. En réfléchissant aux calculs précedents,exprimer AB² en fonction de xa,xb,ya,xb.(le formule doit marcher dans tout les cas)
en déduire Ab=.........................
a la correction nous avions trouver AB=(xb-xa)²+(xb+ya)²
Voila je ne comprends rien :happy2:
Soit (xa,ya) et (xb,yb) les coordonnées de A et B. En réfléchissant aux calculs précedents,exprimer AB² en fonction de xa,xb,ya,xb.(le formule doit marcher dans tout les cas)
en déduire Ab=.........................
a la correction nous avions trouver AB=(xb-xa)²+(xb+ya)²
Voila je ne comprends rien :happy2:
Fais un dessin !
Place deux points A et B au hasard sur le plan muni d'un repère orthonormé. Note les abscisses et ordonnées respectives de A et B.
les abscisses et ordonnées respectives de A et B.
Le but est de trouver la longueur AB en fonction des données. Comment faire ?
Le résultat que tu dois trouver (qui n'est pas celui que tu as mal recopié) est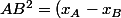^2+(y_A-y_B)^2) .
.
Ce résultat devrait te faire penser à un théorème fameux (=dont tu connais le nom) de géométrie : il se présente sous la même forme qu'un théorème qui dit que, dans certaines conditions, (un truc) au carré + (un machin) au carré = (une chose) au carré.
Vois-tu ce dont je veux parler ?
Si tu vois ce que je veux dire, on pourra rediscuter...
Place deux points A et B au hasard sur le plan muni d'un repère orthonormé. Note
Le but est de trouver la longueur AB en fonction des données. Comment faire ?
Le résultat que tu dois trouver (qui n'est pas celui que tu as mal recopié) est
Ce résultat devrait te faire penser à un théorème fameux (=dont tu connais le nom) de géométrie : il se présente sous la même forme qu'un théorème qui dit que, dans certaines conditions, (un truc) au carré + (un machin) au carré = (une chose) au carré.
Vois-tu ce dont je veux parler ?
Si tu vois ce que je veux dire, on pourra rediscuter...
ju1s a écrit:Bah c'est pythagore :happy2:
Bravo !
ah c'est bon j'ai toruvé y c'est les ordonné et x les abscisse
C'est ça. A et B ce sont tes points (ce sont juste des noms !) et
A partir de là, il faut savoir où est-ce que tu vas exploiter le théorème de Pythagore...
Parce qu'a priori avec tes deux points A et B tu ne vois pas de triangle rectangle... Donc on se demande un peu où on va. D'autre part, comment tes abscisses et tes ordonnées vont bien pouvoir intervenir dans tout ça ??? ...
Pour ça, trace (de force) la droite parallèle à l'axe des abscisses passant par A et la droite parallèle à l'axe des ordonnées passant par B. Appelle O le point d'intersection.
Que remarques-tu sur le triangle AOB ?
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
