Fonction Age of Empires II

[ifebo]

Bonjour
pour gagner au célèbre jeu, je pose la question suivante:
Quelqu'un pourrait il:
1- définir la fonction f donnant la quantité totale y de nourriture obtenue en fonction du temps et du nombre de villageois en service?
2- trouver le nombre optimum de villageois pour obtenir 500 de nourriture en un minimum de temps?
voici les données:

-au départ du jeu, on dispose de 200 de nourriture.
-chaque villageois coute 50 de nourriture. On peut donc produire 4 villageois d'emblée mais...
-il faut 16 secondes pour 'fabriquer' un villageois.
- un villageois produit 10 de nourriture en 22 secondes.

au départ du jeu, on dispose de 3 villageois prêts à agir et à récolter.
on peut par conséquent estimer qu'ils sont sollicités instantanément dès le début de la partie.

On peut donc mettre 5 personnes au travail et attendre d'atteindre 500 ou bien en mettre 6 (on recule de 50 nourriture) puis attendre ou en mettre 7 etc....Cependant il y a ce nombre optimal de villageois à trouver. Une représentation graphique est bienvenue.

Merci

[Cheche]

Je trouve ta question très marrante car souvent les jeux permettent de se passionner aux maths, à l'informatique, ...

Qu'as-tu esssayé de faire ? Où en es-tu ?

[emcee]

bonjour

c'est un peu plus compliqué qu'une simple fonction f (simple au sens "simplement exprimable") car il y a des phénomènes de travail en temps masqué : si par exemple tu décides de créer un villageois dès que tu peux, tu démarres donc avec 7 v et 0 nourriture. A t = 22 secondes tu obtiens 70 de nourriture, tu crées un 8e v. A t = 44", tu obtiens 80 de nourriture, ce qui fait un total de 100. Tu crées un 9e v. Mais tu peux à t=60" créer un 10e v car tu as encore 50 de nourriture. Par la suite ta nourriture augmentera de 100 chaque 22" et encore de 10, 16" plus tard. Etc ... La fonction que tu évoques ressembles probablement à une fonction en escalier pas simple à décrire en une formule succincte.

Par contre pour la stratégie optimale,
1) une stratégie (qu'on va appeler "de base") consiste à ne jamais créer de villageois outre les 3 premiers. Tu peux calculer facilement le temps au bout duquel tu auras N=500
2) pour les autres stratégies : si tu décides de créer un villageois supplémentaire, alors il faut le créer le plus tôt possible. Car en effet, il consomme 50 quel que soit le moment de création mais produira plus tôt s'il est créé plus tôt, donc rien ne sert d'attendre. Donc les autres stratégies consistent simplement à décider du nb total de villageois souhaité, et de simuler le temps nécessaire.

Exemple, avec la stratégie "6 villageois" : j'en crée 3 dès le début. A t=22 j'ai N=50+6*10=110.
A t=44, N=170; etc ... et à t = 286, N=530.

[nodjim]

Ce qui m'étonne dans l'histoire, c'est qu'un villageois ne mange pas...
Il doit manquer une donnée.

[fatal_error]

Ce qui m'étonne dans l'histoire, c'est qu'un villageois ne mange pas...

Bah c'est le moyennage, ils vivent pas très longtemps, ca sert à rien de les nourrir.

Et puis on joue pas aux sims non plus, le but c'est de conquérir la map, pas de fournir une brosse à dent à nos unités (surtout que le paysan c'est quand même le péon de base (dans le jeu))

[nodjim]

Je disais ça parce qu'il n'y a pas de consommation de nourriture autre que "l'achat" d'un villageois. Dans ce cas, ça ne sert à rien de conserver 1 seule unité de nourriture à l'avance, on achète un villageois dès qu'on a 50 unités de nourriture. Dans ce sens, Emcee a donc raison.
Sinon, si le paysan ne mange pas, on ne voit pas pourquoi il s'....à bosser.

[ifebo]

Je trouve ta question très marrante car souvent les jeux permettent de se passionner aux maths, à l'informatique, ...

Qu'as-tu esssayé de faire ? Où en es-tu ?

bjr
Imaginons que j'utilise mes trois villageois exclusivement
abscisses: t le temps
ordonnées: y la nourriture
j'ai une fonction y= at + 200


le villageois produit 10 nourriture en 22 sec.Donc, 27/mn. A trois, ça fait 81.
D'ou le coeff directeur a= 81
y= 81t +200
La nourriture atteint 500 quand 500= 81t+200
soit t= 3,7 mn avec 3 villageois

[ifebo]

bonjour

si par exemple tu décides de créer un villageois dès que tu peux, tu démarres donc avec 7 v et 0 nourriture.

bjr

Et non car on ne peut produire qu'un seul villageois à la fois. ie il faut attendre 16s avant de fabriquer un new villageois.

La fonction que tu évoques ressembles probablement à une fonction en escalier pas simple à décrire en une formule succincte.

oui fonction ayant plutot la forme d'un lame de scie...

pour 3 villageois voir réponse plus haut.
Je fabrique d'emblée un quatrième villageois
la nourriture chute à 150. (200-50)
Pendant les 16s nécessaires à la fabrication du villageois, les 3 autres produisent selon le même coeff de 81/ minutes soit 21,6 en 16s.
donc, dès que le 4° villageois sort, nous avons
y= 81*t+150
y= 81*(16/60)+150
y=171

Mais maintenant j'ai 4 villageois qui travaillent. Mon nouveau coeff a:
a=27*4
a=108
sur ma feuille de papier milimétré, j'arrive à y=500 quand t= 3mn17sec
mais c'est une valeur que j'ai par la lecture de la fonction sur papier. J'ai du mal a faire une fonction mathématique....

[ifebo]

Ce qui m'étonne dans l'histoire, c'est qu'un villageois ne mange pas...
Il doit manquer une donnée.

bjr
il ne manque pas de donnée. le villageois a un cout d'acquisition (50 nourriture) et c'est tout.

[ifebo]

Dans ce cas, ça ne sert à rien de conserver 1 seule unité de nourriture à l'avance, on achète un villageois dès qu'on a 50 unités de nourriture.

et non!!!!! :triste:
a partir d'un moment, il n'est plus rentable de fabriquer d'autre villageois. C'est l'objet même de la question initiale!

[fatal_error]

slt,

alors soit f(t,n) la fonction qui associe à t (le temps) et n (le nombre de villageois) le nombre d'unités de nourriture.
on peut écrire f(t,1) = kt +200
avec k=10/22
de même f(t,2)=2kt+200 et f(t,3)=3kt+200

Maintenant quand on commence à acheter un paysan, on a
f(t,4) = f(t,3) + ce que rapporte le quatrieme - 50
ce que rapporte le quatrieme c'est
k(t - dateCreation_4)
avec dateCreation_4 qui vaut ici 0
-50 car on le paie 50 nourritures.

f(t,5) = f(t,4) + ce que rapporte le cinquieme - 50
le cinquieme rapporte k(t - dateCreation_5) avec dateCreation_5 qui vaut 16 (vu qu'il faut au minimum 16 secondes de délai et qu'on a déjà l'apport nécessaire)

cad f(t,4) = 4kt + C-50 -kdateCreation_4
f(t,5)=5kt + C-50 -k(dateCreation_4+kdateCreation_5)
avec C=200
etc...

où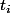 est la date de création du paysan i (avec t_1,t_2,t_3=0; t_4=16)
pour calculer le temps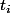 , il faut calculer le temps t tel qu'avec i-1 paysants on ait au moins 50 nourritures ET qu'il n'y a pas déjà un paysan en train d'être construit.
la bouffe rapportée c'est


ensuite, il faut s'assurer que ya pas déjà un péon en train d'etre construit :
si
alors
finsi
et comme ca, tu construis de proche en proche de 4 paysan jusqu'à n.

Enfin, il reste le critère d'arrêt qui est: au bout d'un certain nombre de paysans ca sert à rien d'en créer d'autres, ce qui correspond à pour m paysans, f(t,m)=500 implique ; 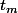correspondant au temps pour atteindre 500 bois
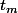étant donné par

[ifebo]

slt,

alors soit f(t,n) la fonction qui associe à t (le temps) et n (le nombre de villageois) le nombre d'unités de nourriture.
on peut écrire f(t,1) = kt +200
avec k=10/22
de même f(t,2)=2kt+200 et f(t,3)=3kt+200

Ouch..j'ai mal a la tête...je n'ai qu un niveau 4eme.
f(t,1)=kt +200
kt est le coefficient directeur, n est ce pas?
Mais pouruoi k=10/22?
Je pensais que k= 27...

[fatal_error]

j'ai pas le même k que toi.

J'ai laissé en seconde.
stu prends kt (avec t en seconde), ben à la 22eme seconde, t'as créé 10/22*22 = 10nourritures, cqui est cqu'on cherche.

[fatal_error]

a copier coller dans un fichier.html

Code: Tout sélectionner


 
   
    AOE
   
   
   
   
 
   

   

    Enable tooltip

function f_inv(u, y, sOffset, K){
   return (y + K.k*sOffset - (K.C-(u-K.nbPeons)*K.pricePeon))/(K.k*u);
}
function f(u, t, sOffset, K){
return u*K.k*t-K.k*sOffset +  K.C-(u-K.nbPeons)*K.pricePeon;
}
function getData(n, k, C, nbPeons, goal, pricePeon, duration){
   var K={
      nbPeons:nbPeons,
      C:C,
      pricePeon:pricePeon,
      duration:duration,
      k:k
   };
   var data=[];
   for(var u=1;utIntersect){tIntersect=tEffectiveOld;}
      var effectiveIntersect=tIntersect+duration;
      
      var goalu=f_inv(u, goal, sOffsetOld+effectiveIntersect, K);
      
      data.push({data:[
         [tIntersect, f(u-1, tIntersect, sOffsetOld, K)-50],
         [effectiveIntersect, f(u, effectiveIntersect, sOffsetOld+effectiveIntersect, K)],
         [goalu, goal]]
         , label:u+'Paysans'
      });
      if(goalu>goaluOld){
         //break;
      }
      sOffsetOld+=effectiveIntersect;
      tEffectiveOld=effectiveIntersect;
      goaluOld=goalu;
   }
   return data;
}


$(function () {
var data=getData(12, 10/22, 200,3, 500,50,16);
    var plot = $.plot($("#placeholder"),
           data, {
               series: {
                   lines: { show: true },
                   points: { show: true }
               },
               grid: { hoverable: true, clickable: true },
               yaxis: { min: 0, max: 520},
               xaxis: { min: 0, max: 250}
             });

    function showTooltip(x, y, contents) {
        $('' + contents + '').css( {
            position: 'absolute',
            display: 'none',
            top: y + 5,
            left: x + 5,
            border: '1px solid #fdd',
            padding: '2px',
            'background-color': '#fee',
            opacity: 0.80
        }).appendTo("body").fadeIn(200);
    }

    var previousPoint = null;
    $("#placeholder").bind("plothover", function (event, pos, item) {

        if ($("#enableTooltip:checked").length > 0) {
            if (item) {
                if (previousPoint != item.dataIndex) {
                    previousPoint = item.dataIndex;
                   
                    $("#tooltip").remove();
                    var x = item.datapoint[0].toFixed(2),
                        y = item.datapoint[1].toFixed(2);
                   
                    showTooltip(item.pageX, item.pageY,
                                item.series.label + " of " + x + " = " + y);
                }
            }
            else {
                $("#tooltip").remove();
                previousPoint = null;           
            }
        }
    });

    $("#placeholder").bind("plotclick", function (event, pos, item) {
        if (item) {
            $("#clickdata").text(" - click point " + item.dataIndex + " in " + item.series.label);
            plot.highlight(item.series, item.datapoint);
        }
    });
});


 


axe des abscisses : temps en secondes
axe des ordonnées : unités de nourritures
on remarque que pdt la création d'un paysan (par exemple le 5eme), le coeff directeur de la droite est le même que celui de la droite correspondant à 4 paysans (les ressources sont accumulées pareil)
le nombre optimal est 7 paysans (avec lesquels sont le plus rapidement atteint les 500 nourritures)