Exercice de math que je ne comprend pas

[Th3darkcatYT]

Bonjour je me nomme Owen , je n'arrive pas a comprendre l'exercice qui peut m'aider ?

Qui pourrais m'aider a comprendre ou me donner les réponse ? Lienvde l'exercice ==> http://www.noelshack.com/2017-08-148762 ... 567978.jpg

[laetidom]

Bonjour je me nomme Owen , je n'arrive pas a comprendre l'exercice qui peut m'aider ?

Qui pourrais m'aider a comprendre ou me donner les réponse ? Lienvde l'exercice ==> http://www.noelshack.com/2017-08-148762 ... 567978.jpg

Bonsoir,

1) 344g pour 2,94euros

2) 312g pour 2,64euros avec 0,30 de réduc en caisse soit 2,34 euros

Quelle solution est plus avantageuse ?


indice : déterminer le prix au kilo, afin d'être en mesure de comparer.

[Th3darkcatYT]

Je n'arrive pas a comprendre

[Th3darkcatYT]

Je comprend pas trop :'(

[WillyCagnes]

bjr

on voit que tu ne fais jamais les courses....
ton choix se porte sur la QUANTITE ou sur le PRIX le moins cher?
1) 344g pour 2,94euros

2) 312g pour 2,34 euros
donc calcule donc le prix au kilo pour chacun afin de comparer le prix le plus interessant
sais tu faire le prix en croix, ou les proportions vu en cours?

[Internaute]

Appelons le prix de bas de l'offre du haut et le prix de base de l'offre du bas. Appelons le taux de produits gratuits prévus pour l'offre du haut, et le remise fixe immédiate de la seconde offre.

Appelons le nombre de boîte mentionné dans l'offre du haut, et celui mentionné dans l'offre du bas. Appelons le poids en grammes de chaque boîte de l'offre du haut et le poids en gramme de chaque boîte de l'offre du bas.

Appelons la quantité (en grammes) de pâté dont Noémie a besoin.

Pour l'offre du haut, le prix au gramme sans prise en compte des dix pour cent offerts est de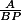 . Après prise en compte de l'avantage de l'offre, la quantité acheté, et donc le dénominateur, doit être multiplié coefficient multiplicateur (le taux auquel on ajoute ). Le prix nets au gramme de l'offre du haut est donc de . Comme il n'y a pas de partie fixe, l'équation représentant le prix à débourser en fonction de la quantité souhaitée est tout simplement .

Pour l'offre du bas, le prix en grammes sans prise en compte de la remise est de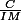 . Le montant de la remise constitue la partie fixe, ce qui fait l'équation représentant le prix à débourser en fonction de la quantité souhaité est .

Pour résumer, le prix à payer en fonction de la quantité en grammes que Noémie veut est représenté par la fonction affine pour l'offre du haut, et par pour l'offre du bas. Faites des calculs algébriques et/ou tracer les courbes afin de déterminer quelle offre est la plus avantageuse, en fonction de la quantité de pâté que Noémie compte acheter.

[laetidom]

Je n'arrive pas à comprendre

Je ne comprend pas trop

Bonjour,

Un petit visuel complémentaire d'aide à la réflexion :



Ainsi, on peut comparer le prix au kilo (1000 g) de chacun des produits.

Bonne journée @ tous !