Exercice difficile

[Luc]

Bonjour,

1. En fait, il est possible et même assez facile de calculer
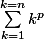
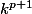
L'idée est d'écrire comme une expression de degré p en k (le terme en s'élimine).
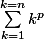
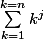
En faisant la somme de 1 à n de chaque membre, on a alors , où A fait intervenir des sommes avec p-1, p-2, ... multipliées par des coefficients. On peut donc calculer de proche en proche, connaissant la valeur des pour
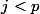
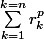
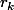
Pour la petite histoire, Newton a donné son nom à une généralisation de ce principe pour calculer où les sont les racines d'un polynôme, en fonction des coefficients de ce polynôme : on appelle de telles sommes des sommes de Newton.

2. Essaie de voir combien de cubes il y a au premier étage du n-ième assemblage.

Luc

[chaa13]

Hey,
Merci luc, tu peux me donner un exemple avec ca :

Pour les cube tu m'a demander seulement le premier étage ? Donc :
r = 1
Imaginons que je veux le nombre de cube au première étage pour la 10 figure :
U0 = 1
U9 = 1 + 9 * 1 (le dixième terme comme on commence a u0)
U9 = 10
Mais en fait ( je crois que je répond a ma question) c'est aussi égale a ça :
U1 = 1
U10 = 1 + (10 -1)*1
U10 = 10

Par contre juste rassure moi dans la figure 3 je vois 10 cube alors qu'il doit en y en avoir seulement 8 !!!!!!
Si y'en a 10 la suite n'est pas logique ?!

Merci d'avance !!!!!

[Luc]

Hey,
Merci luc, tu peux me donner un exemple avec ca :

Attention, à ne pas confondre avec !
Ce que je t'ai dit doit pouvoir te permettre de calculer en écrivant .

Quant à elle, la suite est géométrique et , ce qui permet de calculer la somme des termes d'une suite géométrique, comme tu l'as bien remarqué dans ton post précédent. 363 est correct.

Pour le nombre de cubes, personne n'a dit qu'il fallait montrer . C'est d'ailleurs faux. Mais vérifie tout de même une relation de récurrence, en remarquant que le n-ième empilement est égal au (n-1)-ième empilement + le premier étage.

Luc

[chaa13]

Hey,
J'ai essayer la technique pour : , j'ai donc fait pour k = 1
= 16 ?? Ça devrait faire 1 normalement non ? Ou est-ce que je me suis trompé ?

Et pour les cubes ... Un autre petit problème : si je prend la figure 3 elle est composé de 10 cubes je n'y arrive pas si je fais (3-1) + 3 = 5

Désolé pour toutes ces questions .

Merci d'avance !!!
Charles

[chaa13]

Pas une idée ?

[Luc]

Relis bien ce que j'ai écrit, cela suffit à répondre à tes questions.
Tu sembles avoir du mal à bien comprendre la notation .
Attention à bien écrire exactement ce que tu penses écrire (!)
Essaie de détailler davantage ta démarche et exerce toi au calcul des sommes suivantes avec la technique que je t'ai donné. Il faut exprimer ces sommes en fonction de l'entier n.
S1 =

S2 =

S3 =

S4 =

Luc

[chaa13]

Juste deux petites questions : je peux donner une valuer a n et est-ce que je dois calculer la somme entière ?

Merci d'avance !!!

[Luc]

Juste deux petites questions : je peux donner une valuer a n et est-ce que je dois calculer la somme entière ?

Merci d'avance !!!

Il faut calculer la somme entière. Par exemple S1=1+2+3+...+(n-1)+n.
n est un entier qui peut avoir n'importe quelle valeur.
Tu peux vérifier ton résultat sur des petites valeurs de n.

Luc

[chaa13]

S1 = 1+2+3+4 ...+n
S2 = 1² + 2² +3² .. +n²
S3 = 1^3 ...
??? Il est bizarre ton exo
Sinon pour la somme de ca :
J'ai trouvé un truc mais pas universelle (juste pour k^3):
(Le grande parenthèse englobe toutes la fraction)
Cette formule me permet de calculer la somme mais pas le n ieme terme ...
Il n'y a rien qui marche avec tout (k^4 ,k^10 ...) ?


Merci d'avance !!!!!!!!!!!!!!!!!!!!!!
Charles

[Luc]

J'ai trouvé un truc mais pas universelle (juste pour k^3):
(Le grande parenthèse englobe toutes la fraction)

Tu as donc calculé S3!

Il n'y a rien qui marche avec tout (k^4 ,k^10 ...) ?
Merci d'avance !!!!!!!!!!!!!!!!!!!!!!
Charles

Si, relis mon post sur les sommes de Newton. Par exemple pour k^4, tu développes (k+1)^4-k^4=4k^3+6k^2+4k+1 et tu utilises les valeurs de S0, S1, S2 et S3.

Luc

[chaa13]

Je commençais a S1 et pas a S0
Je me suis trompé aussi ici :
J'ai enlever le -
Donc maintenant si je fais :
C'a ferais : = 81 - 16 = 65 ????
Et on voi que (2+1)^4 = 3^4 = 81 ??
Désolé pour toutes ces question mais la je suis un petit peux perdu

Merci d'avance !!!

[chaa13]

Svp ! Pas une petite idée ?

[chaa13]

Svp !! Juste une petite aide

[Cliffe]

Jme rappelle pas avoir fait sa en 3ème. Nouveau programme ?

[Kikoo <3 Bieber]

Jme rappelle pas avoir fait sa en 3ème. Nouveau programme ?

Nan, mais Charles en veut plus.

Puis d'ailleurs on leur enlève de plus en plus de choses dans le programme.
Comme je le dis souvent, j'ai peur que dans 20 ans les élèves de lycée apprennent à compter.

[chaa13]

Oui je crois qu'il y avait les vecteurs avant non ?

[Elerinna]

Entraîne-toi en éclaireur à manipuler tes séries de sommes en produits : ici

[chaa13]

Merci ! Ça m’occupera !