Equation

par **damien24** » 09 Mar 2007, 11:39

bonjour, je me suis inscrit sur ce site car j'ai une évaluation niveau troisieme bientot (dans le cadre d'une inscription a une formation afpa) et mes cours de maths sont loin ! (j'ai 31 ans et arreté l'école trop tot...); si vous pouviez m'aider a resoudre qques équations ce serait super sympa... en voici deja une (trouvé sur un bouquin d'exercice de 3eme).

( 4x +1)( x 1) ( x 4)( 1 x) 3x (x 1) = 0

par **maf** » 09 Mar 2007, 12:42

(4x+1)(x1) (x4)(1x) 3x(x1) = 0

Ici on voit directement qu'on peut mettre en évidence (x-1)

D'où (x-1)(4x+1+x-4-3x) = 0 donc (x-1)(2x-3) = 0 soit x=1 soit x = 3/2

par **oscar** » 09 Mar 2007, 12:46

Bonjour

A: (4x+1)(x-1) -(x-4)(1-x) -3(x-1)=0
A=.................+(x-4)x-1)
A=(x-1)(4x+1+x-4 -3)=0
......

A=(x-1)(5x-6)=0 Racines...

par **maf** » 09 Mar 2007, 13:39

Il y aurait pas une petite erreur dans ce que tu fais ?? -3x ...

oscar a écrit:Bonjour

A: (4x+1)(x-1) -(x-4)(1-x) -3(x-1)=0
A=.................+(x-4)x-1)
A=(x-1)(4x+1+x-4 -3x)=0
......

A=(x-1)(5x-6)=0 Racines...

par **damien24** » 09 Mar 2007, 14:01

maf a écrit:(4x+1)(x1) (x4)(1x) 3x(x1) = 0

Ici on voit directement qu'on peut mettre en évidence (x-1)

D'où (x-1)(4x+1+x-4-3x) = 0 donc (x-1)(2x-3) = 0 soit x=1 soit x = 3/2

tout d'abord merci pour ton aide... pourrais tu m'expliquer comment as tu obtenu (4x+1+x-4-3x), le 4x ok, le -3x ok, mais je ne comprends pas le
+1+x-4

par **maf** » 09 Mar 2007, 14:06

(4x+1)(x1) (x4)(1x) 3x(x1) = 0

Je vais tout faire par bout :

(4x+1)(x1) la mise en évidence ici était simple
(x4)(1x) = (x-1)(x-4) ici on inverse juste la parenthèse (1-x) grâce au moins qu'il y a devant

3x(x1) = (-3x)(x-1) si je mets des parenthèse pour simplifier ...

Quels sont les éléments qui multiplient (x-1) ??

Tout simplement
(4x+1)
(x-4)
(-3x)
On les aditionne --> (4x+1)+(x-4)-(3x) = (4x+1+x-4-3x) = (2x-3)

par **damien24** » 09 Mar 2007, 15:05

ok merci !
maintenant j'ai : resoudre l'equation 4x²-81=0 et là je ne sais pas comment demarrer...

par **Monsieur23** » 09 Mar 2007, 15:10

4x² = (2x)²
81 = 9² ...

Voilà un petit indice :)

par **damien24** » 09 Mar 2007, 15:23

mais bien sur !! souvent on cherche des complications où il n'y en a pas !!
mais pour celle ci comment procede t on ? :
(3x-1)²-16=0

par **Monsieur23** » 09 Mar 2007, 16:00

Ben de la même façon ...

Ton équation est (3x-1)² - 4² = 0
Factorise, et ensuite, un produit est nul si et seulement un des facteurs est nul :)

par **oscar** » 09 Mar 2007, 17:31

Bonsoir

On a finalement (x-1)(2x-3)=0.

<=> x--1=0<=> x' =1
et 2x-3=0=> x"= 3/2 :marteau:

par **damien24** » 09 Mar 2007, 17:42

(3x-1)²-16=0
(3x-1)²-4²=0
(3x-1-4)(3x-1+4)=0
(3x-5)(3x+3)=0
donc 3x-5=0 et x=5/3
donc 3x+3=0 et x=-1

c'est juste ?

par **Monsieur23** » 09 Mar 2007, 19:02

Oui c'est ça ...

De toutes façons,pour vérifier tu remplace x par les valeurs trouvées, et si ça fait bien 0, c'est gagné :)

par **damien24** » 10 Mar 2007, 15:39

ok super merci de m'aider !!
j'ai un autre soucis pour écrire ce nombre sous forme d'une fraction irreductible b=v2 x v2/v9 ( v étant racine, je ne sais pas comment insérer le symbole)

par **Monsieur23** » 10 Mar 2007, 16:18

Bah ...

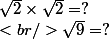
Mr.23

par **damien24** » 10 Mar 2007, 16:33

ok je me rappelais plus que v2² = 2
il y a bien longtemps que je n'ai pas utilisé de racines !
au fait où est la touche racine ?

par **Monsieur23** » 10 Mar 2007, 17:24

Faut écrire en Latex pour écrire comme ça.

Racine de x = \sqrt{x}

Equation

equation

re

re

Qui est en ligne