Bonjour
Je me demandais comment on faisait pour résoudre un équation racine carrée:
Voici l'équation:
23 000= -200 000;)(30-h)+200 000;)h
Équation racine carré à résoudre
8 messages
- Page 1 sur 1
Il faut factoriser -200 000;)(30-h)+200 000;)h
puis élever au carré 23 000= -200 000;)(30-h)+200 000;)h
et simplifier ...
On se retrouvera avec une équation
du type ... = ... au lieu de
... = ... au lieu de  ... +/-
... +/-  ... = ...
... = ...
Attention quand même 30-h doit être positif (pour (30-h))
(30-h))
ainsi que h pour (;)h)
puis élever au carré 23 000= -200 000;)(30-h)+200 000;)h
et simplifier ...
On se retrouvera avec une équation
du type
Attention quand même 30-h doit être positif (pour
ainsi que h pour (;)h)
Mon avatar me fait peur, est-ce normal docteur ?
Kira1310 a écrit:Bonjour
Je me demandais comment on faisait pour résoudre un équation racine carrée:
Voici l'équation:
23 000= -200 000;)(30-h)+200 000;)h
Bonjour,
On pourrait tout d'abord commencer par diviser les deux membres par 1000, histoire de rendre les calculs plus simples.
23 = -200;)(30 - h) + 200;)h
Ce que tu pourrais faire ensuite, c'est prendre 200 en facteur dans le membre de droite, et ensuite diviser le tout par 200.
Donc:
Comme la racine carré d'un nombre n'a de sens que pour un nombre positif, on peut dire que:
Et que
Ensuite, tu peux élever au carré comme bon te semble, et à la fin tu dois vérifier si les solutions obtenues vérifient les conditions sur h, sans quoi l'équation n'admet pas de solution...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Bonjour,
C'est un exercice assez difficile pour un collégien. C'est plutôt de niveau première S. Je vais détailler les calculs tout en glissant discrètement certaines difficultés sous le tapis
Pour éviter de se balader avec des grands nombres tout en te faisant travailler le calcul algébrique,je te propose de poser a=23000 et b=200 000. L'équation devient donc
[CENTER]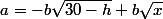 [/CENTER]
[/CENTER]
Déplaçons une racine dans le membre de gauche
[CENTER] .[/CENTER]
.[/CENTER]
Élevons au carré les deux membres afin de chasser les racines
[CENTER] +2ab\sqrt{30-h} = b^2h) .[/CENTER]
.[/CENTER]
Isolons la racine restant dans le membre de gauche
[CENTER]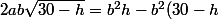) .[/CENTER]
.[/CENTER]
Développons et réduisons le membre de droite
[CENTER]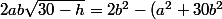) .[/CENTER]
.[/CENTER]
Élevons à nouveau au carré les deux membres de l'équation afin de chasser la dernière racine
[CENTER] = 4b^4h^2+(a^2+30b^2)^2-4b^2h(a^2+30b^2)^2) .[/CENTER]
.[/CENTER]
Développons
[CENTER]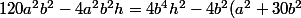h+(a^2+30b^2)^2) .[/CENTER]
.[/CENTER]
Regroupons les termes inconnus dans le membre de gauche, et les termes connus dans le membre de droite
[CENTER]h = 120a^2b^2-(a^2+30b^2)^2) [/CENTER]
[/CENTER]
Regroupons les termes selon les puissances de h, et développons le membre de droite
[CENTER]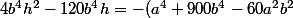) [/CENTER]
[/CENTER]
On reconnait un carré dans la parenthèse
[CENTER]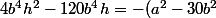^2) [/CENTER]
[/CENTER]
Divisons membre à membre par
[CENTER]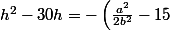^2) [/CENTER]
[/CENTER]
Le membre de gauche peut être vu comme les deux premiers termes du développement du carré de
peut être vu comme les deux premiers termes du développement du carré de  , en effet:
, en effet:
[CENTER]^2=h^2-30h+225) [/CENTER]
[/CENTER]
Ajoutons 225 à chaque membre de l'équation. Nous obtenons
[CENTER]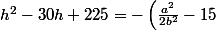^2 + 225 = -\frac{a^4}{4b^4} + 15\frac{a^2}{b^2} + 225 - 225 = \frac{a^2}{b^2}\left(15-\frac{a^2}{4b^2}\right)) ,[/CENTER]
,[/CENTER]
c'est-à-dire
[CENTER]^2 = \frac{a^2}{b^2}\left(15-\frac{a^2}{4b^2}\right)) [/CENTER]
[/CENTER]
Sachant que l'équation) a pour solutions
a pour solutions 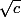 et
et  , et compte tenu du fait que les nombres a et b sont positifs, on a
, et compte tenu du fait que les nombres a et b sont positifs, on a
[CENTER]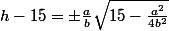 ,[/CENTER]
,[/CENTER]
puis
[CENTER]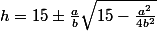 .[/CENTER]
.[/CENTER]
Nous avons donc obtenu deux «solutions»
[CENTER]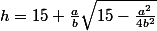 [/CENTER]
[/CENTER]
et
[CENTER]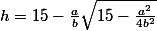 [/CENTER]
[/CENTER]
Toutefois, nous avons élevé au carré à deux reprises les membres de l'équation. Cette opération est susceptible d'ajouter des solutions aux équations résultantes en raison du fait que deux nombres opposés ont même carré.
En testant les deux «solutions» (il y a plus simple) on trouve qu'une seule vérifie l'équation intiale:
[CENTER] [/CENTER]
[/CENTER]
Soit environ .
.
Kira1310 a écrit:23 000= -200 000;)(30-h)+200 000;)h
C'est un exercice assez difficile pour un collégien. C'est plutôt de niveau première S. Je vais détailler les calculs tout en glissant discrètement certaines difficultés sous le tapis
Pour éviter de se balader avec des grands nombres tout en te faisant travailler le calcul algébrique,je te propose de poser a=23000 et b=200 000. L'équation devient donc
[CENTER]
Déplaçons une racine dans le membre de gauche
[CENTER]
Élevons au carré les deux membres afin de chasser les racines
[CENTER]
Isolons la racine restant dans le membre de gauche
[CENTER]
Développons et réduisons le membre de droite
[CENTER]
Élevons à nouveau au carré les deux membres de l'équation afin de chasser la dernière racine
[CENTER]
Développons
[CENTER]
Regroupons les termes inconnus dans le membre de gauche, et les termes connus dans le membre de droite
[CENTER]
Regroupons les termes selon les puissances de h, et développons le membre de droite
[CENTER]
On reconnait un carré dans la parenthèse
[CENTER]
Divisons membre à membre par
[CENTER]
Le membre de gauche
[CENTER]
Ajoutons 225 à chaque membre de l'équation. Nous obtenons
[CENTER]
c'est-à-dire
[CENTER]
Sachant que l'équation
[CENTER]
puis
[CENTER]
Nous avons donc obtenu deux «solutions»
[CENTER]
et
[CENTER]
Toutefois, nous avons élevé au carré à deux reprises les membres de l'équation. Cette opération est susceptible d'ajouter des solutions aux équations résultantes en raison du fait que deux nombres opposés ont même carré.
En testant les deux «solutions» (il y a plus simple) on trouve qu'une seule vérifie l'équation intiale:
[CENTER]
Soit environ
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
