Ensemble de points sur le cercle trigonométrique

[lucadje]

Bonjour à tous. Voici mon problème

soit
T décrivant un arc de cercle

Pourrait on m'expliquer pourquoi l'affirmation suivante est fausse ?

si alors ,

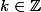
Peut on trouver tel que

Merci

[mathelot]

T est l'arc de cercle AB allant du point A d'abscisse curviligne au point B d'abscisse curviligne


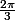
ce n'est pas "pour tout k" mais "il existe k tel que" que l'on devrait écrire
car alpha n'est pas pris modulo 2pi.

[lucadje]

T est l'arc de cercle AB allant du point A d'abscisse curviligne au point B d'abscisse curviligne


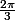
ce n'est pas "pour tout k" mais "il existe k tel que" que l'on devrait écrire
car alpha n'est pas pris modulo 2pi.

Merci mathelot,

Dit comme cela je commence à mieux comprendre.
En effet l'inégalité n'est plus vérifiée, si par exemple
et k=-1

Et pourtant ...
Je ne comprends pas que ceci soit faux

Si sont sur T alors

cela devrait être au moins vrai pour k=0 ?

[mathelot]

tu peux indiquer l'énoncé ?
dans la fonction d'enroulement, les antécédents de
sont constitués de la réunion des

[chombier]

Merci mathelot,

Dit comme cela je commence à mieux comprendre.
En effet l'inégalité n'est plus vérifiée, si par exemple
et k=-1

Et pourtant ...
Je ne comprends pas que ceci soit faux

Si et sont sur T alors

cela devrait être au moins vrai pour k=0 ?

Le "k" de alpha et celui de beta ne sont pas forcément les mêmes. Je me permet de te corriger :

Si et sont sur T alors :



On peut très bien avoir et

Que valent dans ce cas k_1 et k_2 ?