Deux mille sept 2007

[mathelot]

Bonjour,

voiçi le 1er exo des olympiades 2007 de mathématiques de 4ième.
Bon courage. :doh:

On considère le nombre


écrit en copiant 2007 fois les chiffres 2,0,0,7 (N est un nombre de 8028 chiffres)

1. N est il divisible par 9 ?
2. N est il divisible par 81 ?

[stef7272]

Facile il faut utiliser les critères de divisibilité.

[romain1395]

pas du tout

[zauberine]

bah bien sur que si ça a quelque chose a voir !!!tu multiplies 9 par 2007 et t'ajoutes 2*2007 et si c'est divible par neuf alors le nbes et divisible par neuf

[stef7272]

Pas d'accord
Un nombre est divisible par 9 si la somme de ses chiffres est un multiple de 9. Il faut donc additionner tous les chiffres de 20072007 ... et savoir si cette somme est un multiple de 9. Ce qui est facile.

[Clembou]

Bonjour,

voiçi le 1er exo des olympiades 2007 de mathématiques de 4ième.
Bon courage. :doh:

On considère le nombre


écrit en copiant 2007 fois les chiffres 2,0,0,7 (N est un nombre de 8028 chiffres)

1. N est il divisible par 9 ?
2. N est il divisible par 81 ?

Il y a 2007 fois le chiffre 2 et 7. Donc la somme de ces chiffres est 9 et la somme des chiffres que composent N est

Or pour qu'un nombre soit divisible par 9, il faut que la somme de ces chiffres le composant soit divisible par 9.

Or :
Ce nombre est trivialement divisible par 9 (parce qu'on a multiplié 2007 par 9)
et la somme des chiffres de 2007 est 9 donc 18063 est divisible aussi par 81.

Conclusion : N est divisible par 9 et par 81.

[mathelot]

Théorème: Un entier naturel est divisible par 9 si la somme
de ses chiffres est divisible par 9 (et on recommence jusqu'à obtenir un seul chiffre).

La somme des chiffres de N est obtenue en additionnant 2007 fois deux et sept.
La somme des chiffres de N est , donc N est divisible par 9.

on pourra parler aussi d'une méthode de... CM2.

Par contre, je ne vois pas comment vous démontrez que N est divisible par 81. :hum:

[Clembou]

Théorème: Un entier naturel est divisible par 9 si la somme
de ses chiffres est divisible par 9 (et on recommence jusqu'à obtenir un seul chiffre).

La somme des chiffres de N est obtenue en additionnant 2007 fois deux et sept.
La somme des chiffres de N est , donc N est divisible par 9.

on pourra parler aussi d'une méthode de... CM2.

Par contre, je ne vois pas comment vous démontrez que N est divisible par 81. :hum:

Regarde plus en haut : 2007 divisible par 9 et 9 divisible par 9 donc divisible par 81

[mathelot]

je ne comprend pas, certes, la somme des chiffres de N est divisible par 81,
et puis ?

[Clembou]

je ne comprend pas, certes, la somme des chiffres de N est divisible par 81,
et puis ?

N'est-ce pas un des critères de divisibilité par 81 ? Regarde : http://fr.wikipedia.org/wiki/Liste_de_crit%C3%A8res_de_divisibilit%C3%A9 en te souvenant que 3^4 = 81

[Clembou]

Je vais ptêtre faire un petit changement dans mon raisonnement...
Enfin, on prend 2007 et on l'addition 2007 fois
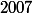
Donc la somme de ces paquets est égale à or divisible par 9 donc divisible par 81 donc N divisible par 81

[mathelot]

N'est-ce pas un des critères de divisibilité par 81 ?

ah, d'accord, je ne connaissais pas.

autre méthode , inspirée du cours primaire:

on pose la division de
,

on trouve comme quotient:



composé de 2007 fois "0223"

et comme reste zéro.

On montre ensuite que Q est divisible par 9.

[mathelot]

autre méthode:


on fait la division de par 2007, on trouve:



Le deuxième facteur Q est divisible par 9 car la somme de ses chiffres vaut 2007.