Comparaison et trigonometrie

[bouyanna]

xet y sont les mesure d angles aigues tel que sinx+siny>3 montrer que cosx+cosy<1 et merci d avance

[annick]

Bonjour,

il y a un truc qui me gêne dans l'énoncé : sinx+siny>3

Je ne vois pas comment c'est possible, sachant que :

sinx<=1
siny<=1

donc :

sinx+siny<=2 et ne pourra jamais avoir sinx+siny>3

[mathelot]

il manque p-e des mesures de longueur des côtés ?

[bouyanna]

oui il y a une faute desole racine de 3 pas 3 merci pour vos remarques

[capitaine nuggets]

et sont des mesure d'angles aiguës tels que . Montrer que .

Salut !

Je te propose de voir les choses géométriquement.

J’appellerais le cercle trigonométrique et le cercle de centre l'origine et de rayon
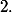
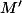
Soient et les points de de coordonnées respectives et .
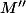
Considérons le point défini par le vecteur .
Exprime , puis en justifiant que , déduis-en alors le résultat voulu.

:+++:

[chan79]

[quote="bouyanna"]xet y sont les mesure d angles aigues tel que sinx+siny> montrer que cosx+cosy=1
Elève tes deux inégalités au carré et ajoute les membre à membre

[mathelot]

aïgu , c e sont des angles au centre du 1er quadrant (<90°)





?

[chan79]

on sait que
sinx+siny>
Supposons que:
cos x + cos y>=1
on aurait

sin²x+sin²y+2 sinx siny >3 et
cos²x+cos²y+2cos x cos y>=1
en additionnant
2+2(sinx sin y+ cosx cosy)>4

sinx sin y+ cosx cosy>1

cos(x-y)>1 impossible

donc cos x +cos y<1

[mathelot]

une démonstration par l'absurde est le truc suivant:

On démontre qu'une propriété entraine, induit, implique "FAUX".

On a supposé que, même si certaines propriétés sont indécidables, rien n'est a la fois Vrai et Faux.

Donc est "FAUX" et sa négation est VRAIE, d'après le tiers-exclu.

[capitaine nuggets]

Salut !

Je te propose de voir les choses géométriquement.

J’appellerais le cercle trigonométrique et le cercle de centre l'origine et de rayon
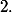
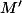
Soient et les points de de coordonnées respectives et .
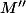
Considérons le point défini par le vecteur .
Exprime , puis en justifiant que , déduis-en alors le résultat voulu.

:+++:

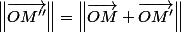
J'étais en train de vérifier ce que j'ai dit et, je me rends compte que je suis allez un peu vite : j'ai malheureusement interprété comme étant .

Du coup, tout ce que j'ai mis est faux !!!

Du coup, j'ai essayé une autre manière ; je reprends tout :

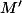
Soient et les points de coordonnées respectives et .
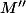
En notant le point défini par , on a par l'identité du parallélogramme :

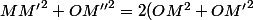[CENTER][/CENTER]

donc et ainsi, .
Ainsi, .
D'où la conclusion :+++:

[bouyanna]

merci tout le monde mais c un exercice pour les olympide des 3 eme college

[mathelot]

considères tu ça comme "finalisé" ? (je voudrai bien savoir d'où vient (***))

pi/3=60°