Bloqué dans une équation

[MATH&ME]

Salut à tous j'ai essayé de resoudre cette equation 1er degre mais il me semble que c'est du 2éme degré, puisqu'en développant le terme gauche on a


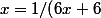j'arrive jusque la et je bloque

[mouette 22]

Salut à tous j'ai essayé de resoudre cette equation 1er degre mais il me semble que c'est du 2éme degré, puisqu'en développant le terme gauche on a


j'arrive jusque la et je bloque

tu ne dois pas avoir x+6 au dénominateur

peux tu écrire tout ton travail ?

ce n'est pas une équation du premier degré en effet

[MATH&ME]

tu ne dois pas avoir x+6 au dénominateur

peux tu écrire tout ton travail ?

ce n'est pas une équation du premier degré en effet

Effectivement et je l'ai trouvé dans un cour pour équation 1er degré .
Alors les etapes je ne m souvient pas vraiment car j'ai utilisé differente pistes , en voila une:










mais comment trouver l'inconnu au 2éme degré.

[Lostounet]

Salut à tous j'ai essayé de resoudre cette equation 1er degre mais il me semble que c'est du 2éme degré, puisqu'en développant le terme gauche on a


j'arrive jusque la et je bloque

Yo salut,
Vu ton travail, je pense que l'équation à résoudre est la suivante:



Est-ce le cas?

Ce n'est pas une équation du premier degré, mais on peut jouer avec pour trouver des solutions avec des outils "collège"...

[MATH&ME]

Merci loustounet ,mais l'équation est .
Reste à voir quel sont les outils college à utiliser ??
ne serais pas par hazard des identités remarquables ????

[Lostounet]

Merci loustounet ,mais l'équation est .
Reste à voir quel sont les outils college à utiliser ??
ne serais pas par hazard des identités remarquables ????

Bien entendu,

Tu multiplies le tout par 6:

4x(x + 6) + 1 = 5

Qui se ramène à:


On peut l'écrire sous la forme suivante, en ajoutant 6^2 et en retranchant 6^2:


Ensuite? :we:

[MATH&ME]

Bien entendu,

Tu multiplies le tout par 6:

4x(x + 6) + 1 = 5

Qui se ramène à:


On peut l'écrire sous la forme suivante, en ajoutant 6^2 et en retranchant 6^2:


Ensuite? :we:

E bein ca se resume à :

[Lostounet]

E bein ca se resume à :

Exactement !

Soit:

[MATH&ME]

comment t'a transformé vers le rationnel. ???

[Lostounet]

comment t'a transformé vers le rationnel. ???

Bah

Et donc l'équation devient (2x + 6)^2 - 40...

En pour faire apparaître un a^2 - b^2, on met sous cette forme

[MATH&ME]

Bah

Et donc l'équation devient (2x + 6)^2 - 40...

En pour faire apparaître un a^2 - b^2, on met sous cette forme

Merci , je vais eesayer de resoudre ca .

[Black Jack]

On peut simplifier un peu ...

En arrivant à : 4x² + 24x - 4 = 0 , on peut commencer par diviser les 2 membres par 4 et traiter alors :

x² + 6x - 1 = 0

(x + 3)² - 9 - 1 = 0

...

:zen:

[MATH&ME]

On peut simplifier un peu ...

En arrivant à : 4x² + 24x - 4 = 0 , on peut commencer par diviser les 2 membres par 4 et traiter alors :

x² + 6x - 1 = 0

(x + 3)² - 9 - 1 = 0

...

:zen:

Je ne sais pas resoudre des equations de 2éme degré , mais ca serait benefique de le savoir , comment proceder BLACKJACK ?????

[mouette 22]

Je ne sais pas resoudre des equations de 2éme degré , mais ca serait benefique de le savoir , comment proceder BLACKJACK ?????

Salam! Si vraiment tu veux t'y mettre va sur Wikipedia ""équation du second degré "Je pense qu 'avec ta volonté tu vas y arriver !
cependant ici Blackjack écrit

A²-B² :lol3: ce qui fait que tu peux résoudre cette équation sans passer par "ax²+bx+c"

[Black Jack]

Je ne sais pas resoudre des equations de 2éme degré , mais ca serait benefique de le savoir , comment proceder BLACKJACK ?????

Dans le cas présent, c'est immédiat

(x + 3)² - 9 - 1 = 0
(x + 3)² = 10
x+3 = +/- V10 (avec V pour racine carrée).
x = -3 +/- V10

S:{-3-V10 ; -3+V10}
******
Ou bien autrement :
(x + 3)² - 9 - 1 = 0
(x + 3)² - 10 = 0
(x + 3)² - (V10)² = 0

et on se rappelle que a²-b² = (a-b)(a+b)
avec ici : a = x+3 et b = V10
...

:zen:

[MATH&ME]

Merci je vais m'y mettre .