Bonjour,
Pourriez-vous me dire comment démontrer que l'aire d'un triangle est égale au produit du demi-périmétre par le rayon du cercle inscrit.
Aire Du Triangle
8 messages
- Page 1 sur 1
Bonsoir (ou plutôt bonne nuit vu l'heure),
Soit un triangle quelconque ABC d'aire S, O le centre du cercle circonscrit au triangle de rayon R et I le centre du cercle inscrit dans le triangle de rayon r.
On note a, b et c les côtés opposés à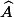 ,
, 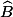 , et
, et 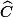 respectivement, et p le demi-périmètre de ABC.
respectivement, et p le demi-périmètre de ABC.
Je te conseille de faire une figure pour suivre.
D'après le théorème de l'angle au centre :
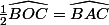 si A est sur le grand arc.
si A est sur le grand arc.
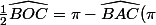) si A est sur le petit arc.
si A est sur le petit arc.
Donc dans tous les cas,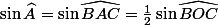
Comme le triangle BOC est isocèle, on a :
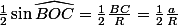
D'où :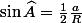 et
et 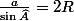
Sachant que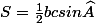 , on a
, on a 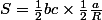 .
.
D'où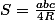
Enfin, en décomposant le triangle ABC en trois triangles, BOC, AOC, AOB dont les aires sont respectivement ,
,  et
et  , il vient :
, il vient :
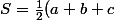r=pr)
Voilà voilà. Un peu compliqué pour du niveau collège, plaqué comme ça je trouve.
Soit un triangle quelconque ABC d'aire S, O le centre du cercle circonscrit au triangle de rayon R et I le centre du cercle inscrit dans le triangle de rayon r.
On note a, b et c les côtés opposés à
Je te conseille de faire une figure pour suivre.
D'après le théorème de l'angle au centre :
Donc dans tous les cas,
Comme le triangle BOC est isocèle, on a :
D'où :
Sachant que
D'où
Enfin, en décomposant le triangle ABC en trois triangles, BOC, AOC, AOB dont les aires sont respectivement
Voilà voilà. Un peu compliqué pour du niveau collège, plaqué comme ça je trouve.
Aire Du Triangle
T'inquiète pas. Ce n'est pas du niveau de 4ème.
Mais le début va m'aider à poursuivre les recherches.
Je n'ai pas encore appris les sinus. Ce sera en 3ème.
Merci encore
Mais le début va m'aider à poursuivre les recherches.
Je n'ai pas encore appris les sinus. Ce sera en 3ème.
Merci encore
Bonjour
ABC est un triangle ; I est le centre du cercle inscrit ;
I se projette orthogonalement en A', B' et C' respectivement sur [BC], [CA] et [AB].
On obtient 6 triangles rectangles dont la somme des aires est l'aire de ABC.
De plus, IA'=IB'=IC'=rayon du cercle inscrit ;
AB'=AC' ; BA'=BC' et CA'=CB' (propriété des bissectrices).
Il doit être facile de terminer.
ABC est un triangle ; I est le centre du cercle inscrit ;
I se projette orthogonalement en A', B' et C' respectivement sur [BC], [CA] et [AB].
On obtient 6 triangles rectangles dont la somme des aires est l'aire de ABC.
De plus, IA'=IB'=IC'=rayon du cercle inscrit ;
AB'=AC' ; BA'=BC' et CA'=CB' (propriété des bissectrices).
Il doit être facile de terminer.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
