nan
rejette un oeil aux égalités que je t'ai données pour te rappeler la propriété de Thalès
DM de 4eme tres dur
51 messages
- Page 3 sur 3 - 1, 2, 3
effectivement,  est juste. mais je ne suis pas sûr que ça nous aide vraiment :lol3:
est juste. mais je ne suis pas sûr que ça nous aide vraiment :lol3:
reprenons :
Nous pouvons calculer instantanément l'aire du triangle ABC en faisant . On aimerait pouvoir faire de même avec le triangle AB'C' connaissant sa base B'C' (donnée en énoncé), mais nous ne connaissons pas sa hauteur AH'... (dans ta rédaction il faudra aussi démontrer que AH' est la hauteur de AB'C' mais ça n'est pas le coeur du problème).
. On aimerait pouvoir faire de même avec le triangle AB'C' connaissant sa base B'C' (donnée en énoncé), mais nous ne connaissons pas sa hauteur AH'... (dans ta rédaction il faudra aussi démontrer que AH' est la hauteur de AB'C' mais ça n'est pas le coeur du problème).

Nous cherchons la longueur :
:
dans le triangle AB'C', du fait que BC et B'C' soient parallèles, on a alors en utilisant le théorème de Thalès les égalités :
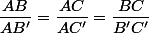
Par ailleurs, comme H appartient à (BC) et H' appartient à (B'C'), droites qui sont parallèles, on peut donc affirmer que (BH) est parallèle à (B'H'). Ainsi, dans le triangle AB'H', en appliquant le théorème de Thalès (eh oui encore!), on a l'égalité :

Tu te retrouves donc avec deux suites d'égalités qui ont des termes en commun. Cela te permets alors d'en déduire une égalité simple permettant d'exprimer la longueur en fonction des longueurs que l'on te donne en énoncé, à savoir
en fonction des longueurs que l'on te donne en énoncé, à savoir 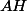 ,
, 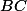 et
et 
reprenons :
Nous pouvons calculer instantanément l'aire du triangle ABC en faisant

Nous cherchons la longueur
dans le triangle AB'C', du fait que BC et B'C' soient parallèles, on a alors en utilisant le théorème de Thalès les égalités :
Par ailleurs, comme H appartient à (BC) et H' appartient à (B'C'), droites qui sont parallèles, on peut donc affirmer que (BH) est parallèle à (B'H'). Ainsi, dans le triangle AB'H', en appliquant le théorème de Thalès (eh oui encore!), on a l'égalité :
Tu te retrouves donc avec deux suites d'égalités qui ont des termes en commun. Cela te permets alors d'en déduire une égalité simple permettant d'exprimer la longueur
Frednight a écrit:effectivement,est juste. mais je ne suis pas sûr que ça nous aide vraiment :lol3:
reprenons :
Nous pouvons calculer instantanément l'aire du triangle ABC en faisant. On aimerait pouvoir faire de même avec le triangle AB'C' connaissant sa base B'C' (donnée en énoncé), mais nous ne connaissons pas sa hauteur AH'... (dans ta rédaction il faudra aussi démontrer que AH' est la hauteur de AB'C' mais ça n'est pas le coeur du problème).
Nous cherchons la longueur:
dans le triangle AB'C', du fait que BC et B'C' soient parallèles, on a alors en utilisant le théorème de Thalès les égalités :
Par ailleurs, comme H appartient à (BC) et H' appartient à (B'C'), droites qui sont parallèles, on peut donc affirmer que (BH) est parallèle à (B'H'). Ainsi, dans le triangle AB'H', en appliquant le théorème de Thalès (eh oui encore!), on a l'égalité :
Tu te retrouves donc avec deux suites d'égalités qui ont des termes en commun. Cela te permets alors d'en déduire une égalité simple permettant d'exprimer la longueuren fonction des longueurs que l'on te donne en énoncé, à savoir
,
et
donc attend on a B'C' qui fais 9cm et AH' qui fais 8cm vu que AH fais 4cm, AH//AH' donc AH' est egal 8cm non ??
des équations précédentes tu déduis donc que :

L'aire du triangle AB'C' est alors égale à :

contre pour le petit triangle .
pour le petit triangle .
en faisant le rapport des l'aire du grand triangle AB'C' par celle du petit triangle ABC, on trouve alors^2)
C'est uen propriété des triangles semblables : lorsque l'on multiplie les longueurs d'une figure donnée par un certain rapport (ici ), l'aire de la figure initiale est multipliée par le carré de ce même rapport.
), l'aire de la figure initiale est multipliée par le carré de ce même rapport.
L'aire du triangle AB'C' est alors égale à :
contre
en faisant le rapport des l'aire du grand triangle AB'C' par celle du petit triangle ABC, on trouve alors
C'est uen propriété des triangles semblables : lorsque l'on multiplie les longueurs d'une figure donnée par un certain rapport (ici
51 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
