Je vous invite à un débat!
51 messages
- Page 2 sur 3 - 1, 2, 3
Robot a écrit:Toujours la même erreur, toujours au même endroit. Tu tournes en rond !
Au fait, qui sonttels que
et que
? D'où les sors-tu ?
Informations pratiques:
Pour calculer le chiffre
Regardé vous Lemme 0a?
Êtes-vous d'accord avec elle?
Tu ne réponds pas aux questions. je répète :
1°) Tu affirmes^n= (a''n+1)^n) (remarque :
(remarque :_{[2]}=a''n+1) ). Comment le montres tu ?
). Comment le montres tu ?
2°) Qui sont les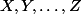 que tu sors de ton chapeau sans justification ?
que tu sors de ton chapeau sans justification ?
TU JOUES A CACHE-CACHE AVEC TON ERREUR, MAIS ELLE EST TOUJOURS LA ET BIEN LA.
Sur l'utilisation de ton lemme 0a, j'avais déjà fait l'objection suivante dans l'autre fil : pour appliquer ce lemme, il faudrait avoir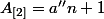 . C'est sous cette hypothèse qu'on pourrait en déduire
. C'est sous cette hypothèse qu'on pourrait en déduire _{(3)}=a'') . Or, tout ce que tu as, c'est
. Or, tout ce que tu as, c'est _{[2]} = \left( (a''n+1)^n\right)_{[2]}) .
.
Explique alors comment tu appliques le lemme 0a (en détail, sans manoeuvrer une fois de plus pour cacher ton erreur).
PS : ton lemme 0a est une trivialité. Ce n'est bien entendu pas lui que je conteste, mais l'application que tu prétends en faire, et qui est complètement fausse.
1°) Tu affirmes
2°) Qui sont les
TU JOUES A CACHE-CACHE AVEC TON ERREUR, MAIS ELLE EST TOUJOURS LA ET BIEN LA.
Sur l'utilisation de ton lemme 0a, j'avais déjà fait l'objection suivante dans l'autre fil : pour appliquer ce lemme, il faudrait avoir
Explique alors comment tu appliques le lemme 0a (en détail, sans manoeuvrer une fois de plus pour cacher ton erreur).
PS : ton lemme 0a est une trivialité. Ce n'est bien entendu pas lui que je conteste, mais l'application que tu prétends en faire, et qui est complètement fausse.
Robot a écrit:Tu ne réponds pas aux questions. je répète :
1°) Tu affirmes(remarque :
). Comment le montres tu ?
2°) Qui sont lesque tu sors de ton chapeau sans justification ?
TU JOUES A CACHE-CACHE AVEC TON ERREUR, MAIS ELLE EST TOUJOURS LA ET BIEN LA.
Sur l'utilisation de ton lemme 0a, j'avais déjà fait l'objection suivante dans l'autre fil : pour appliquer ce lemme, il faudrait avoir. C'est sous cette hypothèse qu'on pourrait en déduire
. Or, tout ce que tu as, c'est
.
Explique alors comment tu appliques le lemme 0a (en détail, sans manoeuvrer une fois de plus pour cacher ton erreur).
PS : ton lemme 0a est une trivialité. Ce n'est bien entendu pas lui que je conteste, mais l'application que tu prétends en faire, et qui est complètement fausse.
1°) Oui, parce que
2°)
Lemma.
Bon, tu es indécrottable. Tes réponses ne valent rien. Tu ne démontres rien du tout. N'importe qui se donnant la peine de creuser un peu pourra vérifier que ton argument est vide.
J'ai mis un commentaire sur vixra. Au moins tu ne pourras pas continuer à prétendre que personne n'a trouvé d'erreur dans ton texte.
J'ai mis un commentaire sur vixra. Au moins tu ne pourras pas continuer à prétendre que personne n'a trouvé d'erreur dans ton texte.
Robot a écrit:Bon, tu es indécrottable. Tes réponses ne valent rien. Tu ne démontres rien du tout. N'importe qui se donnant la peine de creuser un peu pourra vérifier que ton argument est vide.
J'ai mis un commentaire sur vixra. Au moins tu ne pourras pas continuer à prétendre que personne n'a trouvé d'erreur dans ton texte.
J'ai prouvé l'égalité A''=a'':
mais vous ai pas trouvé une erreur!
Tu n'as pas prouvé =a''n+1) .
.
Tu as seulement prouvé_{[2]}=\left((a''n+1)^n\right)_{[2]}) .
.
Donc, tout ton raisonnement s'écroule. Tu as cherché par différents moyens à camoufler ce trou, sans aucun succès.
J'ai trouvé au moins une erreur dans ton raisonnement. Tes dénégations n'y changeront rien.
Tu invites à un débat, mais tu persistes contre toute évidence à ne pas reconnaître ton erreur flagrante. A ce point-là, je vois deux possibilités d'explication pour ton comportement :
1°) tu ne vois pas la faute dans ton raisonnement, et donc tu es complètement incompétent en mathématiques.
ou
2°) tu vois la faute dans ton raisonnement, et donc tu es malhonnête intellectuellement.
J'hésite entre les deux explications.
PS : je surenchéris. Je te promets 500 pour une preuve irréfutable de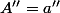 . :ptdr:
. :ptdr:
PS2 : pour te simplifier l'écriture de cette preuve irréfutable, je te répète les points sur lesquels je suis d'accord ( est un nombre premier) :
est un nombre premier) :
1° :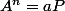
2° :_{[k+2]}= 1)
3° :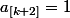
4° :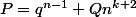
5° :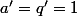
6° :_{[2]}=\left((a''n+1)^n\right)_{[2]})
7° : Pour tout entier , si
, si 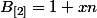 , alors
, alors _{(3)}=x) .
.
Tu as seulement prouvé
Donc, tout ton raisonnement s'écroule. Tu as cherché par différents moyens à camoufler ce trou, sans aucun succès.
J'ai trouvé au moins une erreur dans ton raisonnement. Tes dénégations n'y changeront rien.
Tu invites à un débat, mais tu persistes contre toute évidence à ne pas reconnaître ton erreur flagrante. A ce point-là, je vois deux possibilités d'explication pour ton comportement :
1°) tu ne vois pas la faute dans ton raisonnement, et donc tu es complètement incompétent en mathématiques.
ou
2°) tu vois la faute dans ton raisonnement, et donc tu es malhonnête intellectuellement.
J'hésite entre les deux explications.
PS : je surenchéris. Je te promets 500 pour une preuve irréfutable de
PS2 : pour te simplifier l'écriture de cette preuve irréfutable, je te répète les points sur lesquels je suis d'accord (
1° :
2° :
3° :
4° :
5° :
6° :
7° : Pour tout entier
Robot a écrit:Tu n'as pas prouvé.
Tu as seulement prouvé.
Donc, tout ton raisonnement s'écroule. Tu as cherché par différents moyens à camoufler ce trou, sans aucun succès.
J'ai trouvé au moins une erreur dans ton raisonnement. Tes dénégations n'y changeront rien.
Tu invites à un débat, mais tu persistes contre toute évidence à ne pas reconnaître ton erreur flagrante. A ce point-là, je vois deux possibilités d'explication pour ton comportement :
1°) tu ne vois pas la faute dans ton raisonnement, et donc tu es complètement incompétent en mathématiques.
ou
2°) tu vois la faute dans ton raisonnement, et donc tu es malhonnête intellectuellement.
J'hésite entre les deux explications.
PS : je surenchéris. Je te promets 500 pour une preuve irréfutable de. :ptdr:
PS2 : pour te simplifier l'écriture de cette preuve irréfutable, je te répète les points sur lesquels je suis d'accord (est un nombre premier) :
1° :
2° :
3° :
4° :
5° :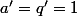
6° :
7° : Pour tout entier, si
, alors
.
En principe, je l'ai répondu à toutes vos questions. Mais je vais les répéter aux fiers et arrogants 400 génies principalement de «Institut de Mathématiques de Toulouse»:
Je les mets au défi de débattre une honte!
Mais 500 euros, vous vous laisser - ils seront toujours venir dans maniable.
Remarque. Votre erreur insignifiante: la conclusion 3°
Alors, Lemme:
Preuve.
Dès réception du produit
nous laissons tomber les troisième, les quatrième et ainsi de suite chiffres dans tous les facteurs premiers du nombre A (et, par conséquent, dans aP) avec recevoir (en tenant compte également Lemme 0a°) lidentité :
Doù (selon le lemme 0a°)
Victor Sorokine a écrit:En principe, je l'ai répondu à toutes vos questions.
Non, en tout cas pas de réponse pertinente.
Victor Sorokine a écrit:Mais 500 euros, vous vous laisser - ils seront toujours venir dans maniable.
Phrase incompréhensible. Enfin, pas d'importance.
Victor Sorokine a écrit:Remarque. Votre erreur insignifiante: la conclusion 3° encore nécessaire de prouver.
D'accord, c'est une erreur de ma part. Un copié collé trop hâtif.J'exclus ce 3°) des choses que j'admets.
Victor Sorokine a écrit:Dès réception du produitdans le côté droit de légalité de Fermat en forme
Je ne sais toujours pas ce qu'est
Robot a écrit:qui sonttels que
et que
? D'où les sors-tu ?
je n'ai obtenu pour réponse (et encore, en insistant lourdement) que
Victor Sorokine a écrit:2°),
,
sont les facteurs de
.
Quels facteurs ? Faut il comprendre
Robot a écrit:1) Je ne sais toujours pas ce qu'est. Quelle décomposition en facteurs de
utilises-tu pour écrire ce
? Ca fait partie des questions pour lesquelles je n'ai obtenu aucune réponse pertinente. A ma question
2) Quels facteurs ? Faut il comprendre? Mais on ne sait pas que
. Donc, ce n'est pas ça. Alors, une nouvelle fois, qui sont
1) V. déterminations: A_{/t/}, où A=pq...r, est le produit p_{[t]}*q_{[t]}*...*r_{[t]}.
Les troisièmes chiffres dans ces expressions ne dépendent pas de A''' et de a'''!
2) Tous les facteurs premiers dans
Victor Sorokine a écrit:(n facteurs).
D'après ta définition (qui pose quelques problèmes, par ailleurs),
Victor Sorokine a écrit: 2) Tous les facteurs premiers danset dans
.
Ah bon, il y a donc
Robot a écrit:D'après ta définition (qui pose quelques problèmes, par ailleurs),est défini à partir d'une décomposition de
en produit. Quelle factorisation de
en produit de
facteurs utilises-tu pour écrire cette égalité ? D'après ce que je comprends, tu dis que tu as une factorisation en produit de
facteurs
tels que
. Je ne comprends pas d'où vient cette factorisation. Peux-tu l'expliquer ?
2) Ah bon, il y a doncfacteurs premiers dans
? (Tu avais écrit plus haut, je te le rappelle dans ton message du 17/11 à 8h35, que les
sont au nombre de
.) C'est-à-dire que
est premier ? Pourquoi ?
2) facteurs premiers est un autre sujet : rejet des troisième, quatrième etc. chiffres.
Victor Sorokine a écrit:(
facteurs!) car
. Les nombres
peuvent être composite. Cela vous étonne?
2) facteurs premiers est un autre sujet : rejet des troisième, quatrième etc. chiffres.
Cela ne m'étonne absolument pas. Ce qui m'étonne, c'est que tu tiennes des propos incohérents : tout le monde peut voir que de tes affirmations successives on déduit que A est premier. Tu t'es trompé, donc ?
Je suis aussi très embêté que tu ne répondes pas du tout à mes questions. Tu renonces à éclaircir ta démonstration ? Tu t'es rendu compte que ça cloche ? Sinon, tu devrais pouvoir répondre à ma question. C'est au sujet de ce que tu as écrit :
Victor Sorokine a écrit:(n facteurs).
Je te repose une nouvelle fois la question.
Robot a écrit:D'après ta définition (qui pose quelques problèmes, par ailleurs),est défini à partir d'une décomposition de
en produit. Quelle factorisation de
en produit de
facteurs utilises-tu pour écrire cette égalité ? D'après ce que je comprends, tu dis que tu as une factorisation en produit de
facteurs
tels que
. Je ne comprends pas d'où vient cette factorisation. Peux-tu l'expliquer ?
Je te fais remarquer que tu ne peux pas prendre les
J'aimerais une vraie réponse. Faute de quoi, je serais (et tous les lecteurs de ce fil avec moi) amené à conclure que tu ne réponds pas parce que tu ne sais pas répondre ..; et donc que ta "démonstration" se casse la figure ici.
Joker62 a écrit:Hello,
Moi je trouve la preuve de Viktor très juste et brillante.
Voilà merci
Alors Joker62, tu peux sans doute répondre à la question que je pose sans arriver à obtenir de réponse, et que je rappelle (si tu n'as pas la réponse, c'est que tu ne comprends pas cette "preuve très juste", et on peut alors se poser des questions sur la pertinence de ton appréciation).
Robot a écrit:D'après ta définition (qui pose quelques problèmes, par ailleurs),est défini à partir d'une décomposition de
en produit. Quelle factorisation de
en produit de
facteurs utilises-tu pour écrire l'égalité suivante :
(n facteurs) ?
D'après ce que je comprends, tu dis que tu as une factorisation en produit defacteurs
tels que
. Je ne comprends pas d'où vient cette factorisation. Peux-tu l'expliquer ?
Ah au fait, Joker62, ma promesse de récompense de 500 pour une démonstration convaincante de
(je soupçonne fort que Joker veuille simplement troller... Tu as du courage robot, mais ça me paraît inutile. Certaines personnes, même face à une preuve rigoureuse, ne peuve pas reconnaitre leurs erreurs.)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
51 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
