Lierre Aeripz a écrit:J'aime beaucoup les preuves qui utilisent toute une théorie pour la démonstration mais où cette théorie est absente des hypothèses et de la conclusion. Je trouve que c'est là que les mathématiques sont les plus belles : quand une théorie s'applique à une autre, alors que ni le résultat, ni le problème initial n'ont de rapport avec celle-là. Ces énoncés sont plutôt rares.
De nombreux théorèmes sont très jolis (cf vos cours de maths), mais la plupart du temps les hypothèses les placent déjà dans le cadre de la théorie.
Voici quelques exemples.
- L'égalité de Parceval
Pour )
,
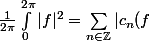|^2)
Où l'on a bien sûr  = \frac{1}{2\pi}\int_0^{2\pi} f(t) e^{-i n t} dt)
La démonstration de cette égalité utilise la géométrie euclidienne et le fait que les polynômes trigonométriques sont denses dans l'espaces des fonctions continues 
périodiques
Cet énoncé ne rentre pas complètement de ceux dont j'ai parlé puisque les 
n'ont pas de raison d'être sans la théorie de Fourier...
Cette égalité permet de calculer des sommes de séries tout à fait non triviales ()
, )
, etc, sans formule générale pour les )
cependant).
Ce théorème n'est pas tout à fait de ceux que j'ai cité plus haut, mais c'est le seul que j'ai en tête qui est de niveau L2 ou spé. (il y en a d'autre, aidez-moi !)
- Le théorème de Dirichlet
Pour a et b entiers premier entre eux, il existe une infinité de nombre premiers dans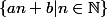 
.
La démonstration de ce théorème utilise de nombreux résultat d'analyse et en particulier sur les séries, alors que l'énoncé est de l'arithmétique pure.
Une preuve arithmétique à été trouvée mais bien plus tard et sans doute beaucoup plus ardue.
- Le théorème de Goodstein
(cf. internet pour la définition des suites de Goodstein)
Ce théorème est un petit miracle. On définit une famille de suite d'entier, les suite de Goodstein, qui ont tout pour tendre vers l'infini. Le calcul montre qu'elles prennent effectivement des valeurs faramineuses. Le miracle, c'est que toutes ces suites tendent en fait vers zéro.
La démonstration utilise la théorie des ordinaux de Cantor. L'idée est que ces suites ne peuvent pas être efficacement majorées dans 
, il faut utiliser des éléments plus grand que tout élément de . On les trouve dans les ordinaux. Aussi grand qu'ils soient, ils conservent une propriété fondamentale des entiers : il n'existe pas de suite strictement décroissante d'ordinaux.
Ce qui rend ce théorème intéressant (et beau), c'est vraiment sa preuve.
- Le théorème d'Ax
Soit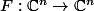 
polynômiale, c'est-à-dire que les fonctions coordonnées sont des polynômes en les n variables.
Si F est injective, alors elle est surjective. Impressionnant, non ?
La démonstration de ce théroème est tout entièrement basée sur le logique formelle (théorème de complétude de Gödel, théorèmes sur l'élimination des quantificateurs, etc).
Plus particulièrement, on utilise le résultat suivant : tout énoncé pouvant s'écrire en logique du premier ordre avec +, -, x, 0, et 1 valable dans au moins un corps algébriquement clos de caractéristique nulle est valable dans tout corps algébriquement clos de caractéristique nulle.
Le théorème est joli, mais la preuve est vraiment bluffante. Grosso modo, on parvient en changeant de corps à restreindre F à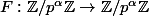 
, et dans le cas de cardinaux finis, il est évident que l'injectivité entraine la surjectivité.
Bonjour
Désolé d'exhumer un post déjà ancien, mais nouveau sur ce forum, je découvre...
Je reviens sur le théorème de Goodstein : moi aussi, il me fascine, mais il y a un truc qui m'y gène bcp. Je vais le formulier d'une manière volontairement naïve (je ne suis pas mathématicien) :
- On a beau entasser des entiers faramineux, démentiels, "après", il y a toujours un entier.
, le premier ordinal transfini, n'est pas un entier, on ne le touchera jamais en comptant vers le haut.
- Or, dans la démonstration de Goodstein, c'est dans le sens inverse : on a bien une suite décroissante dordinaux transfinis, mais, redescendus à
, pouf ! On retombe dans le domaine entier, si je puis dire.
Il y a, comment dire, une dissymétrie qui me choque.
Merci de tout éclairage.
