Pour résoudre une équation ou inéquation, la première étape indispensable est : on compare à 0.
On obtient ici
 Avec le discriminant
Avec le discriminantC'est du second degré de la forme
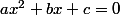
, le discriminant est
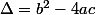
et s'il est positif, les solutions sont

Comme ici b est pair, on peut passer par le discriminant réduit : en posant
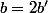
, cela fait
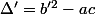
et les solutions sont
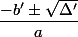
Ici, a=5, b=14 (donc b'=7), c=-91, on a donc
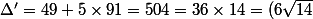^2)
Ce qui donne les deux solutions
 Sans utiliser le discriminant :
Sans utiliser le discriminant : La seule façon de résoudre est de factoriser, puis d'appliquer la règle "un produit est nul ssi l'un des facteurs est nul".
Commençons par "virer" le mutiplicateur du

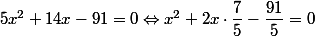
Le principe est de faire apparaître des identités remarquables( parce que ça, on sait factoriser).
Remarquons alors que

est le début de

: on peut toujours écrire

=
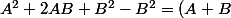^2-B^2)
Ici,
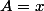
et
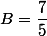
.
On obtient alors
^2-\dfrac{49}{25}-\dfrac{91}{5}=0)
C'est-à-dire
^2-\dfrac{504}{25}=0)
Remarquons que
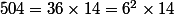
, on peut donc écrire
^2\quad-\quad\Big(\dfrac{6\sqrt{14}}{5}\Big)^2=0)
On reconnaît là l'identité remarquable
(A+B))
, ce qui permet de factoriser
\Big(x+\dfrac{7}{5}+\dfrac{6\sqrt{14}}{5}\Big)=0)
Avec un peu d'ajustement
\Big(x-\dfrac{-7-6\sqrt{14}}{5}\Big)=0)
On termine : un produit est nul ssi l'un des facteurs est nul.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
