Pour quelles valeurs de
Une équation avec des nombres premiers
12 messages
- Page 1 sur 1
Une équation avec des nombres premiers
Bonjour,
Pour quelles valeurs de , l'expression
, l'expression 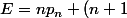p_{n+1}+(n+2)p_{n+2}) est un nombre carré parfait , où
est un nombre carré parfait , où 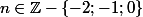 et
et 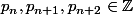 sont des nombres premiers consécutifs.
sont des nombres premiers consécutifs.
Pour quelles valeurs de
Modifié en dernier par Dacu le 19 Avr 2016, 05:45, modifié 2 fois.
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Une équation avec des nombres premiers
Salut,
J'ai rien résolu du tout, mais le " " me semble... douteux... : c'est quoi
" me semble... douteux... : c'est quoi  ? et
? et  ?
?
(pour moi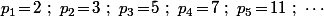 )
)
J'ai rien résolu du tout, mais le "
(pour moi
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Une équation avec des nombres premiers
Bonjour,
Je suis malheureusement, incapable d'y répondre. Sais tu si c'est possible au moins ? Parce que pour moi on ne connait l'expression de pn donc ce n'est pas possible. Il y a peut-être une solution mais je ne la connais pas
Ou l'as tu trouvé?
Et oui, je pense aussi que les entiers relatifs ne sont pas valide ici ^^
Je suis malheureusement, incapable d'y répondre. Sais tu si c'est possible au moins ? Parce que pour moi on ne connait l'expression de pn donc ce n'est pas possible. Il y a peut-être une solution mais je ne la connais pas

Ou l'as tu trouvé?
Et oui, je pense aussi que les entiers relatifs ne sont pas valide ici ^^
Re: Une équation avec des nombres premiers
Ben314 a écrit:Salut,
J'ai rien résolu du tout, mais le "" me semble... douteux... : c'est quoi
? et
?
(pour moi)
Salut,
Mille pardons!Je rectifié:
......... ,
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Une équation avec des nombres premiers
Un nombre premier est un entier naturel (tiré de wikipédia), je ne suis pas sur que on puisse faire cela ^^
Sinon ou l'as tu trouvé ? ^^
Sinon ou l'as tu trouvé ? ^^
Re: Une équation avec des nombres premiers
rikoo a écrit:Un nombre premier est un entier naturel (tiré de wikipédia), je ne suis pas sur que on puisse faire cela ^^
Sinon ou l'as tu trouvé ? ^^
Salut,
"Wolfram Alpha":
https://www.wolframalpha.com/input/?i=-17
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Une équation avec des nombres premiers
Ce n'est pas parce que un programme informatique dit que un nombre est premier qu'il l'est forcément.
N'empêche que tu m'as toujours pas dit ou tu l'as trouvé !
N'empêche que tu m'as toujours pas dit ou tu l'as trouvé !
Re: Une équation avec des nombres premiers
n ne peut pas valoir -1 (n+1=0) ni -2 (n+2=0).
Et au final le Z n'apporte rien, puisque c'est le même résultat pour n positif ou négatif. IN* est très bien.
Et au final le Z n'apporte rien, puisque c'est le même résultat pour n positif ou négatif. IN* est très bien.
Re: Une équation avec des nombres premiers
nodgim a écrit:n ne peut pas valoir -1 (n+1=0) ni -2 (n+2=0).
Et au final le Z n'apporte rien, puisque c'est le même résultat pour n positif ou négatif. IN* est très bien.
Salut,
Vous avez raison! Je l'ai changé! Merci beaucoup!
Je pense qu'il est bon d'expansion pour
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Une équation avec des nombres premiers
Dacu, connais tu la réponse ?
J'ai trouvé 2 solutions, avec n = 2 (2*3+3*5+4*7=7²) et n = 68 (68*337+69*347+70*349=267²) en essayant les nombres premiers jusqu'à 1000. Il y en a peut être d'autres.
J'ai trouvé 2 solutions, avec n = 2 (2*3+3*5+4*7=7²) et n = 68 (68*337+69*347+70*349=267²) en essayant les nombres premiers jusqu'à 1000. Il y en a peut être d'autres.
Re: Une équation avec des nombres premiers
nodgim a écrit:Dacu, connais tu la réponse ?
J'ai trouvé 2 solutions, avec n = 2 (2*3+3*5+4*7=7²) et n = 68 (68*337+69*347+70*349=267²) en essayant les nombres premiers jusqu'à 1000. Il y en a peut être d'autres.
Salut,
J'étudie si oui ou non il y a un nombre infini de solutions.
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Une équation avec des nombres premiers
D'accord, et bien bon courage alors ^^
Moi je chercherai d'abord du côté des nombres parfait et voir quel(les) formules/théorèmes ils existent dessus. C'est peut-être pas la bonne méthode mais bon si ça peut aider
Moi je chercherai d'abord du côté des nombres parfait et voir quel(les) formules/théorèmes ils existent dessus. C'est peut-être pas la bonne méthode mais bon si ça peut aider
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
