Une autre équation avec des nombres premiers

[Dacu]

Bonjour,

Pour quelles valeurs de , l'expression est un nombre carré parfait , où 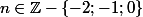et 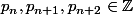sont des nombres premiers consécutifs.

[rikoo]

Bonjour,

Toujours aucune idée x)
Mais as tu trouvé la solution de l'autre ? ^^

[Dacu]

Bonjour,

Toujours aucune idée x)
Mais as tu trouvé la solution de l'autre ? ^^

Bon matin,

Dans les deux cas je recherche le nombre de solutions possibles.

[nodgim]

Si tu parvenais à même seulement répondre à cette question, ce serait un apport important en maths sur la connaissance des nombres premiers !

[Romy]

Pour quelles valeurs de , l'expression est un nombre carré parfait , où et sont des nombres premiers consécutifs.

D'où vient l'équation ? Si: au temps d'Euclide où 1 était premier. Aujourd'hui, l'équation est fausse pour car 1 n'est pas un entier premier. Peut-être y a t-il des solutions ?

[rikoo]

Bonjour,

"Dans notre système de numération habituel, le chiffre des unités d'un carré parfait ne peut être que 0, 1, 4, 5, 6 ou 9. En base douze, il serait obligatoirement 0, 1, 4 ou 9."

Je me disais que çà serait peut-être une bonne idée d'appliquer le modulo 10 sur ton équation. Voilà c'est tout ^^