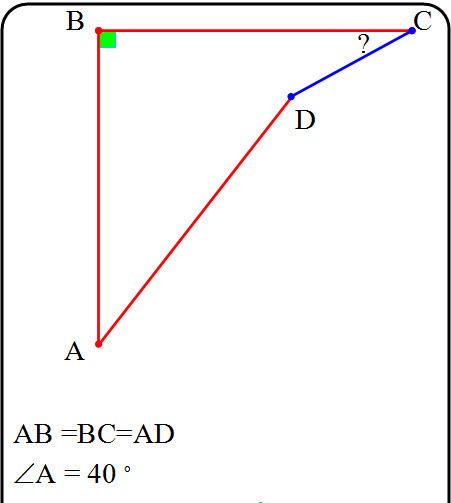
Trouver l'angle C

[brhum.moh]

[CENTER] [/CENTER]

trouver l'angle C

[Imod]

Tu places le point E à droite de (AB) de façon à ce que ABE soit équilatéral , après c'est du calcul d'angle niveau collège :zen:

Imod

[Ben314]

Salut,
Tu es sûr de ton coup ?
Perso, avec A=40°, je trouve un angle C qui n'a rien de remarquable.
Y'a qu'avec A=30°,45°,60° que je trouve des C "simples" (15°,45°,75°)

[brhum.moh]

Salut,
Tu es sûr de ton coup ?
Perso, avec A=40°, je trouve un angle C qui n'a rien de remarquable.
Y'a qu'avec A=30°,45°,60° que je trouve des C "simples" (15°,45°,75°)

:mur:

A=20°

[Ben314]

A=20°

=> C=5.236833517229641° (selon géogébra) qui, à priori, ne me semble pas trop "remarquable"...

Sauf erreur, en général, on a

[brhum.moh]

salut Ben314

Voilà autant que je l'ai (mon professeur de toute façon) a disparu. Comment puis-je résoudre ce problème?

[Lostounet]

=> C=5.236833517229641° (selon géogébra) qui, à priori, ne me semble pas trop "remarquable"...

Sauf erreur, en général, on a

Hello,

J'ai essayé d'exprimer A en fonction de C en passant par les cotés avec la loi des sin et Al-Kashi (les cotés se sont simplifiés), ça me donne une formule horrible en Arcsin. Comment trouves-tu une expression simple? (je peux montrer mes calculs...)

[Imod]

C'est assez simple , on prend des segments rouges de taille 1 et on projette orthogonalement D en H sur (AB) et en K sur (BC) . Alors AH=cos et DH=sin donc CK=1-sin et DK=1-cos .

Imod

[Lostounet]

Ah oui c'est simple!
Ceci dit, c'est bizarre l'expression que je trouve...