Mathusalem a écrit:Est-ce qu'il est possible de degager de la preuve un concept majeur qui rend la construction impossible ?
Je connais une preuve, mais j'imagine qu'il peut y en avoir d'autres... Je pense quand même qu'elle ressemble à la preuve originale.
C'est une preuve algébrique qui commence par montrer qu'avec un compas et une règle (non graduée), on ne peut construire uniquement des longueurs qui sont les éléments d'une tour d'extensions quadratiques sur
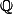
:
 \ \subset\ E_2 = {\mathbb Q}(\sqrt{x_0}, \sqrt{x_1}) \ \subset\ \cdots \ \subset\ E_n = {\mathbb Q}(\sqrt{x_0}, \sqrt{x_1}, ... \sqrt{x_{n-1}}))
où
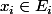
. Cela vient tout simplement du fait que les équations de cercles "correspondent" aux équations de degré 2.
Il faut remarquer que, pour tout i, la dimension de
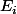
sur Q est
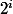
. (Comme il s'agit de corps, on parle de degré d'extension, et non dimension, mais c'est pareil...)
Un corollaire est que, si un nombre est constructible à la règle et au compas, alors il est algébrique sur

et le degré de son polynôme minimal est une puissance de 2.
Par exemple, le nombre
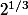
a pour polynôme minimal
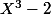
. Or 3 n'est pas une puissance de 2, donc
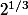
n'est pas constructible à la règle et au compas. Idem pour

, qui n'est même pas algébrique...
Passons maintenant au problème de trisection d'un angle.En fait, construire un angle est équivalent à construire ses sinus et cosinus. La question revient à se demander si
)
et
)
appartiennent à une tour d'extensions quadratiques sur le corps engendré par
)
et
)
. Et la réponse est non, car
)
est algébrique de degré 3 (comme
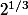
!) avec pour polynôme "minimal générique" (*)
/4)
.
(vous connaissez la relation
 = 4\cos^3(t) - 3\cos(t))
! )
Bref, l'obstruction est que 3 n'est pas une puissance de 2. :zen:
(*) c'est effectivement le polynôme minimal en général, mais sur des cas particuliers, le polynôme minimal peut être de degré inférieur... ce qui signifie qu'en général, on ne pourra pas trisecter un angle, mais que sur des cas très particuliers c'est possible.
