Trajectoire d'interception
24 messages
- Page 1 sur 2 - 1, 2
Trajectoire d'interception
Bonjour à tous
Je cherche l'équation qui décrit une trajectoire d'interception entre un objet en trajectoire rectiligne, vers un autre objet sur une orbite circulaire (Genre un vaisseau [avec trajectoire rectiligne] en direction d'une planète).
Je me doute que l'équation doit être assez complexe.
Ce que je cherche, c'est la position de la planète au moment de l'interception en connaissant :
*la position initiale de la planète et sa vitesse angulaire,
*la position de départ du vaisseau et sa vitesse constante.
J'ai fais des recherches, mais tout ce que j'ai trouve c'est une équation qui décrit un trajectoire d'interception entre deux objets ayant une trajectoire rectiligne.
Je cherche l'équation qui décrit une trajectoire d'interception entre un objet en trajectoire rectiligne, vers un autre objet sur une orbite circulaire (Genre un vaisseau [avec trajectoire rectiligne] en direction d'une planète).
Je me doute que l'équation doit être assez complexe.
Ce que je cherche, c'est la position de la planète au moment de l'interception en connaissant :
*la position initiale de la planète et sa vitesse angulaire,
*la position de départ du vaisseau et sa vitesse constante.
J'ai fais des recherches, mais tout ce que j'ai trouve c'est une équation qui décrit un trajectoire d'interception entre deux objets ayant une trajectoire rectiligne.
J'ai du mal exposer mon problème ;)
Pour le vaisseau (M), j'ai sa position (Xm,Ym) de départ et sa vitesse (v). Sa direction n'est pas définie. Elle le sera en fonction de la solution de lieu d'interception,
pour la planète (N), je connais sa position (Xn, Yn) en fonction du temps (t).
On va dire que la vitesse linéaire de M est supérieure à celle de N. ce qui implique qu'il y a forcément un point d'interception possible.
Pour le vaisseau (M), j'ai sa position (Xm,Ym) de départ et sa vitesse (v). Sa direction n'est pas définie. Elle le sera en fonction de la solution de lieu d'interception,
pour la planète (N), je connais sa position (Xn, Yn) en fonction du temps (t).
On va dire que la vitesse linéaire de M est supérieure à celle de N. ce qui implique qu'il y a forcément un point d'interception possible.
Je cherche la position de N au moment de l'interception.
A noter que la position de départ de M peut si situer à l'intérieur ou à l'extérieure de l'orbite.
Et aussi, je ne l'ai pas dit plus haut, mais je connais évidemment la distance planète-centre de l'orbite.
En fait, il faut imaginer qu'à un instant T on lance un vaisseau à destination d'une planète.
Le problème est du même genre que celui-ci : http://www.maths-forum.com/showthread.php?t=139192&highlight=trajectoire+d%27interception
sauf que je cherche a connaitre la position de N (qui a une trajectoire circulaire, et non linéaire comme décrit dans le sujet ci-dessus).
A noter que la position de départ de M peut si situer à l'intérieur ou à l'extérieure de l'orbite.
Et aussi, je ne l'ai pas dit plus haut, mais je connais évidemment la distance planète-centre de l'orbite.
En fait, il faut imaginer qu'à un instant T on lance un vaisseau à destination d'une planète.
Le problème est du même genre que celui-ci : http://www.maths-forum.com/showthread.php?t=139192&highlight=trajectoire+d%27interception
sauf que je cherche a connaitre la position de N (qui a une trajectoire circulaire, et non linéaire comme décrit dans le sujet ci-dessus).
Pas évident de comprendre ce que tu veux faire :hein: . Si on utilise la représentation paramétrique :
Trajectoire de N en fonction du temps :: \ \left\{\begin{array}{rcl} x_N (t) & = & x_C + R \cos \left ( \omega t + \alpha_0 \right )\\ y_N (t) & = & y_C + R \sin \left ( \omega t + \alpha_0 \right ) \end{array}\right.)
Avec) le centre du cercle,
le centre du cercle,  le rayon,
le rayon,  la vitesse angulaire et
la vitesse angulaire et 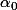 la position de
la position de  pour
pour 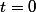 .
.
Trajectoire de M en fonction du temps : : \ \left\{\begin{array}{rcl} x_M (t) & = & x_0 + v_x t\\ y_M (t) & = & y_0 + v_y t \end{array}\right.) avec
avec  .
.
Avec) la position de
la position de  pour
pour 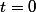 et
et 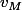 la vitesse de
la vitesse de  .
.
Le point (ou un point) d'intersection, noté au temps
au temps  vérifie :
vérifie :
[CENTER] & = & x_0 + v_x t_I\\ y_I(t_I) & = & y_0 + v_y t_I\\ x_I(t_I) & = & x_C + R \cos \left ( \omega t_I + \alpha_0\right )\\ y_I(t_I) & = & y_C + R \sin \left ( \omega t_I + \alpha_0\right ) \end{array}\right.) [/CENTER]
[/CENTER]
Il faut alors résoudre le système :\\ y_0 + v_y t_I & = & y_C + R \sin \left ( \omega t_I + \alpha_0\right ) \\ v_M & = & \sqrt{{v_x}^2+{v_y}^2} \end{array}\right.) . Les inconnues étant
. Les inconnues étant  .
.
Trajectoire de N en fonction du temps :
Avec
Trajectoire de M en fonction du temps :
Avec
Le point (ou un point) d'intersection, noté
[CENTER]
Il faut alors résoudre le système :
Merci Cliffe. Je crois que j'ai compris et que ça répond à ma question. Je vais potasser ça demain à tête reposée.
en fait, après quelques réflexions, c'est de tI dont j'aurais le plus besoin.).
grace à tI, je pourrais connaitre la position (Xn et Yn) de la planète. et de là en déduire Vx et Vy (Vm étant connu)
est-il possible d'avoir l'équation en fonction de tI ?
en fait, après quelques réflexions, c'est de tI dont j'aurais le plus besoin.).
grace à tI, je pourrais connaitre la position (Xn et Yn) de la planète. et de là en déduire Vx et Vy (Vm étant connu)
est-il possible d'avoir l'équation en fonction de tI ?
Je suis en train d'écrire un jeu (en php et java), dans lequel il y aura ce genre de déplacements.
Je ne sais pas ce que c'est une "formule littérale approchée".
Et si on passe par les dérivées/primitives ou autres intégrales, y'a pas un moyen de trouver tI ? J'ai pas étudié ce genre de truc, mais je comprends vaguement le principe.
Je ne sais pas ce que c'est une "formule littérale approchée".
Et si on passe par les dérivées/primitives ou autres intégrales, y'a pas un moyen de trouver tI ? J'ai pas étudié ce genre de truc, mais je comprends vaguement le principe.
En repartant des équations de Cliffe, on peut avancer un peu sur le problème : Si on fixe la vitesse du bolide à V et que l'on cherche sa direction alpha, les équations deviennent :
 t_I = x_C + R \cos \left ( \omega t_I + \alpha_0\right ))
 t_I = y_C + R \sin \left ( \omega t_I + \alpha_0\right ))
En vrai, si on se place par rapport à l'axe reliant la position initiale du projectile et le centre de l'orbite du vaisseau, on peut toujours se ramener à yC = y0 = 0, et l'angle alpha étant l'angle que fait la trajectoire rectiligne du projectile par rapport à cet axe, on a en fait :
 t_I = x_C-x_0 + R \cos \left ( \omega t_I + \alpha_0\right ))
 t_I = R \sin \left ( \omega t_I + \alpha_0\right ))
En manipulant ces deux équations I et II, on peut en tirer deux choses :
1) II/I nous donne:
 = \frac{R \sin \left ( \omega t_I + \alpha_0\right )}{x_C-x_0 + R \cos \left ( \omega t_I + \alpha_0\right )})
On a donc exprimé la direction solution en fonction du moment de l'impact (si tant est qu'on arrive à le trouver).
2) I²+II² donne :
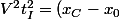^2+R^2+2R(x_C-x_0)\cos \left ( \omega t_I + \alpha_0\right ))
On a éliminé l'angle ici, on a donc une équation permettant de calculer le temps d'impact donc découlera l'angle solution avec l'équation obtenue plus haut.
Ici pas de solution analytique, il faut utiliser une méthode numérique, mais on peut tout de même analyser un peu plus cette équation. Si on note f(tI) le second membre, on voit que :
)^2 \leq f(t_I) \leq (R+(x_c-x_0))^2)
Comme le membre de gauche V²tI² est strictement croissante et couvre de 0 à +infini, on est sûr d'avoir au minimum une solution dans tous les cas.
Pour aller encore un peu plus loin, on cherche donc les points d'intersection entre une parabole (terme de gauche), et une fonction périodique de période 2pi/omega (terme de droite). Le(s) points d'intersections vont avoir lieu lorsque V²tI² entre dans la fenêtre)^2,(R+(x_c-x_0))^2\right]) , si dans cet intervalle de temps le membre de droite est relativement plat/stable, il n'y aura qu'une solution, à l'inverse si le membre de droite "a le temps" d'osciller, il y aura à vue de nez à peu près autant de solution que d'oscillations.
, si dans cet intervalle de temps le membre de droite est relativement plat/stable, il n'y aura qu'une solution, à l'inverse si le membre de droite "a le temps" d'osciller, il y aura à vue de nez à peu près autant de solution que d'oscillations.
En résumé, plus la pulsation omega du satellite va être grande devant la vitesse V du projectile, et plus cette équation aura de solutions, c'est à dire plus le nombre de temps et de points de collisions possibles sera important. (le lieu de collision découlant du temps et de l'angle qui découle lui même du temps via la première équation)
Damien
En vrai, si on se place par rapport à l'axe reliant la position initiale du projectile et le centre de l'orbite du vaisseau, on peut toujours se ramener à yC = y0 = 0, et l'angle alpha étant l'angle que fait la trajectoire rectiligne du projectile par rapport à cet axe, on a en fait :
En manipulant ces deux équations I et II, on peut en tirer deux choses :
1) II/I nous donne:
On a donc exprimé la direction solution en fonction du moment de l'impact (si tant est qu'on arrive à le trouver).
2) I²+II² donne :
On a éliminé l'angle ici, on a donc une équation permettant de calculer le temps d'impact donc découlera l'angle solution avec l'équation obtenue plus haut.
Ici pas de solution analytique, il faut utiliser une méthode numérique, mais on peut tout de même analyser un peu plus cette équation. Si on note f(tI) le second membre, on voit que :
Comme le membre de gauche V²tI² est strictement croissante et couvre de 0 à +infini, on est sûr d'avoir au minimum une solution dans tous les cas.
Pour aller encore un peu plus loin, on cherche donc les points d'intersection entre une parabole (terme de gauche), et une fonction périodique de période 2pi/omega (terme de droite). Le(s) points d'intersections vont avoir lieu lorsque V²tI² entre dans la fenêtre
En résumé, plus la pulsation omega du satellite va être grande devant la vitesse V du projectile, et plus cette équation aura de solutions, c'est à dire plus le nombre de temps et de points de collisions possibles sera important. (le lieu de collision découlant du temps et de l'angle qui découle lui même du temps via la première équation)
Damien
Cliffe a écrit:On parle de point qui n'ont pas de dimension, comment peu til y avoir plus de 2 collisions ?
Cette réflexion vaut si l'angle de la trajectoire est fixé préalablement alors là oui au plus il peut y avoir deux collisions, mais ce n'est pas le cas ici... Et cette propriété de variabilité de l'angle s'est transférée dans l'équation sur t_I quand on l'a éliminé.
Mais pour essayer d'imager.
Si on part disons d'une solutions, je sais par exemple que pour un certain t_I et un angle alpha disons alpha > 0, je peux avoir une collision ? Et la distance parcourue sera un peu plus grande donc j'aurai nécessairement un t_I'>t_I car le chemin est un peu plus long. mais est-ce que c'est possible de retrouver sur ce point le satellite, et bien oui si le satellite a eu le temps de faire tout le tour de son orbite et revenir dans la zone dans l'intervalle de temps tI'-tI. La pulsation doit donc être importante. Et en fait on voit que plus la pulsation sera grande, et plus il y aura d'angles possibles pour une collision, sans même parler des collisions possible sur la face opposée de l'orbite. La règle c'est donc plutôt à peu près deux fois plus de collisions que d'oscillation dans l'intervalle cité plus haut.

Edit : D'ailleurs la courbe que tu as dessinée correspondant à l'équation montre bien 5 solutions et donc 5 points d'intersections ! (car l'équation I de la tangente a toujours une et une seule solution pour l'angle quel que soit t_I).
Damien
OK mais à priori l'angle était à déterminer également.
Sûrement mais ça va surement être un truc sordide avec des parties entières, pas sûr que ça serve beaucoup.
Ca doit être quelque chose du style)^2-(R-(x_c-x_0))^2}/V*\omega/\pi) = Int(\sqrt{4R(x_c-x_0)}\frac{\omega}{V\pi}))
à une unité près selon la phase initiale de l'orbite, mais bon pas convaincu que ça serve à grand chose d'exprimer le nombre exact exact. Cette formule signifie juste deux fois le nombre de périodes du terme de droite dans le temps où la parabole a mis à traverser la fenêtre citée plus haut.
Damien
jmb59 a écrit:Ce que je cherche, c'est la position de la planète au moment de l'interception en connaissant :
*la position initiale de la planète et sa vitesse angulaire,
*la position de départ du vaisseau et sa vitesse constante.
jmb59 a écrit:Sinon, on peut donner le nombre de solutions sous forme littéral non ?
Sûrement mais ça va surement être un truc sordide avec des parties entières, pas sûr que ça serve beaucoup.
Ca doit être quelque chose du style
à une unité près selon la phase initiale de l'orbite, mais bon pas convaincu que ça serve à grand chose d'exprimer le nombre exact exact. Cette formule signifie juste deux fois le nombre de périodes du terme de droite dans le temps où la parabole a mis à traverser la fenêtre citée plus haut.
Damien
Merci pour vos équations, et pour le temps que vous passez pour moi.
Je pensais que ce problème était compliqué, mais pas à ce point.
Si je comprends bien (dites moi si je me trompe), il n'y a pas d'équation du type tI=...
Quoiqu'on fasse, on se retrouve toujours avec tI dans les deux parties de l'équation. Ce qui fait que je ne saurais pas, d'un point de vue programmation, trouver tI.
Pour la fenêtre du temps d'interception, il me suffit de calculer la distance entre M et le point du cercle le plus proche d'une part, et le point du cercle le plus éloigné d'autre part. Ce qui correspond à ce que tu disais DamX dans ton post de 10h38.
A l'aide de cette fenêtre, je peux toujours faire plusieurs essais afin de trouver le temps d'interception le plus proche. Faudra que je fasse des tests. Pour l'instant rien n'est codé, j'en suis a l'étude de faisabilité.
Ces calculs sont-ils valables si M se trouve à l'intérieur de l'orbite ?
Sinon, si ça peut vous aider, le temps de trajet est inférieur à une révolution de la planète, et la distance entre M et N est inférieure à 15 fois le rayon. Mais je ne pense pas que ça change quelque chose aux équations.
Je pensais que ce problème était compliqué, mais pas à ce point.
Si je comprends bien (dites moi si je me trompe), il n'y a pas d'équation du type tI=...
Quoiqu'on fasse, on se retrouve toujours avec tI dans les deux parties de l'équation. Ce qui fait que je ne saurais pas, d'un point de vue programmation, trouver tI.
Pour la fenêtre du temps d'interception, il me suffit de calculer la distance entre M et le point du cercle le plus proche d'une part, et le point du cercle le plus éloigné d'autre part. Ce qui correspond à ce que tu disais DamX dans ton post de 10h38.
A l'aide de cette fenêtre, je peux toujours faire plusieurs essais afin de trouver le temps d'interception le plus proche. Faudra que je fasse des tests. Pour l'instant rien n'est codé, j'en suis a l'étude de faisabilité.
Ces calculs sont-ils valables si M se trouve à l'intérieur de l'orbite ?
Sinon, si ça peut vous aider, le temps de trajet est inférieur à une révolution de la planète, et la distance entre M et N est inférieure à 15 fois le rayon. Mais je ne pense pas que ça change quelque chose aux équations.
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 [/CENTER]
[/CENTER] [/CENTER]
[/CENTER]