Un problème me trotte dans la tête de temps à autres depuis un certain temps (ça doit se compter en années, maintenant).
L'idée est partie d'un vague projet de jeu dans lequel un bonhomme se balade sur une carte composée de cases. Le plus courant dans ce genre de cas est d'avoir une carte carrée ou rectangulaire, avec des cases carrés (ou plus rarement hexagonales), et dont les bords sont soit des "bouts du monde" infranchissables, soit des passages vers le bord opposé, comme si on se baladait sur un tore.
Seulement, j'avais envie que le joueur n'ai pas vraiment d'autre point de repère que son "champs de vision" (les cases qui s'affichent autour de son personnage sur son écran), et pour corser les inévitables tentatives de cartographie, j'ai eu l'idée de rendre la carte globalement non-euclidienne (mais euclidienne localement).
Je m'explique : si le personnage se balade sur un cube (ou son patron) dont les faces seraient chacune un élément de la carte. Les arrêtes ne sont pas visibles et les sommets ne sont ni accessibles ni visible dans le champs de vision du personnage. Dans ce cas, tout laisse à croire au joueur qu'il évolue sur une surface euclidienne tant qu'il n'a pas fait le tour d'un sommet (et tenté de cartographier son chemin).
Le tétraèdre, l'octaèdre et l’icosaèdre se prêtent également bien à cet exercice, sauf qu'il faut paver les faces avec des triangles ou des hexagones plutôt qu'avec des carrés.
Jusque là, le personnage évolue sur une surface qui lui semble euclidienne mais qui dans son ensemble est une approximation discrète d'une sphère.
Maintenant, comme j'ai un certain goût pour l'originalité, je me suis demandé s'il était possible de faire la même chose pour un tore.
Pour essayer de poser la question en termes plus mathématiques, je cherche donc un (ou plusieurs) polyèdre(s)
- qui serait topologiquement un tore (et qui s'en rapprocherait le plus possible)
- dont on pourrait paver la surface avec une continuité cohérente dans le pavage de part et d'autre des arrêtes, exception faite des sommets (et de leurs abords)
Vous noterez qu'il n'est pas nécessaire que les tuiles du pavages s'arrêtent aux arrêtes. Une tuile peut être à cheval sur deux faces.
Jusqu'à maintenant, j'ai trouvé trois solutions :
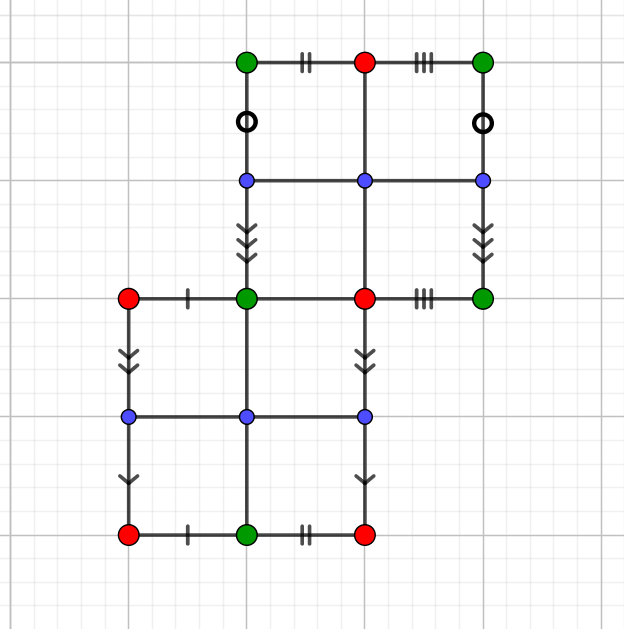
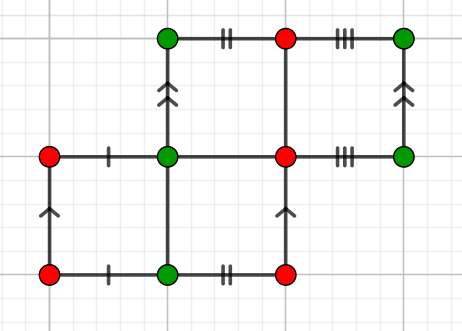
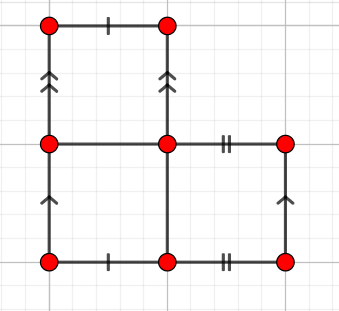
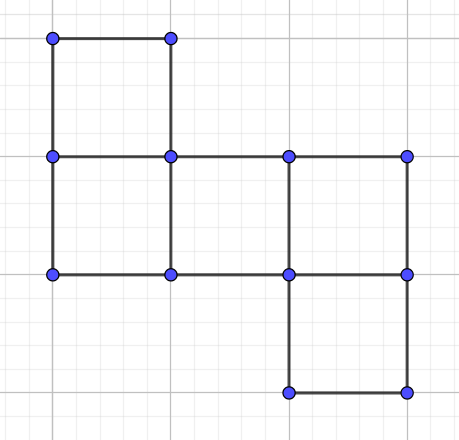
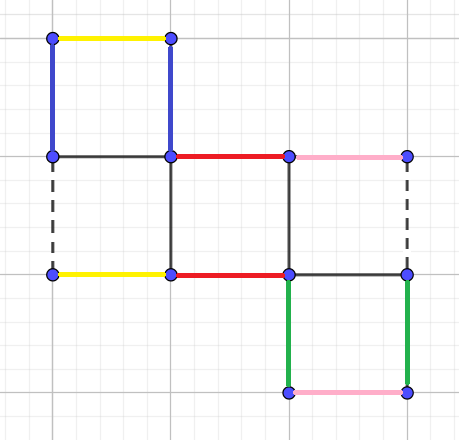
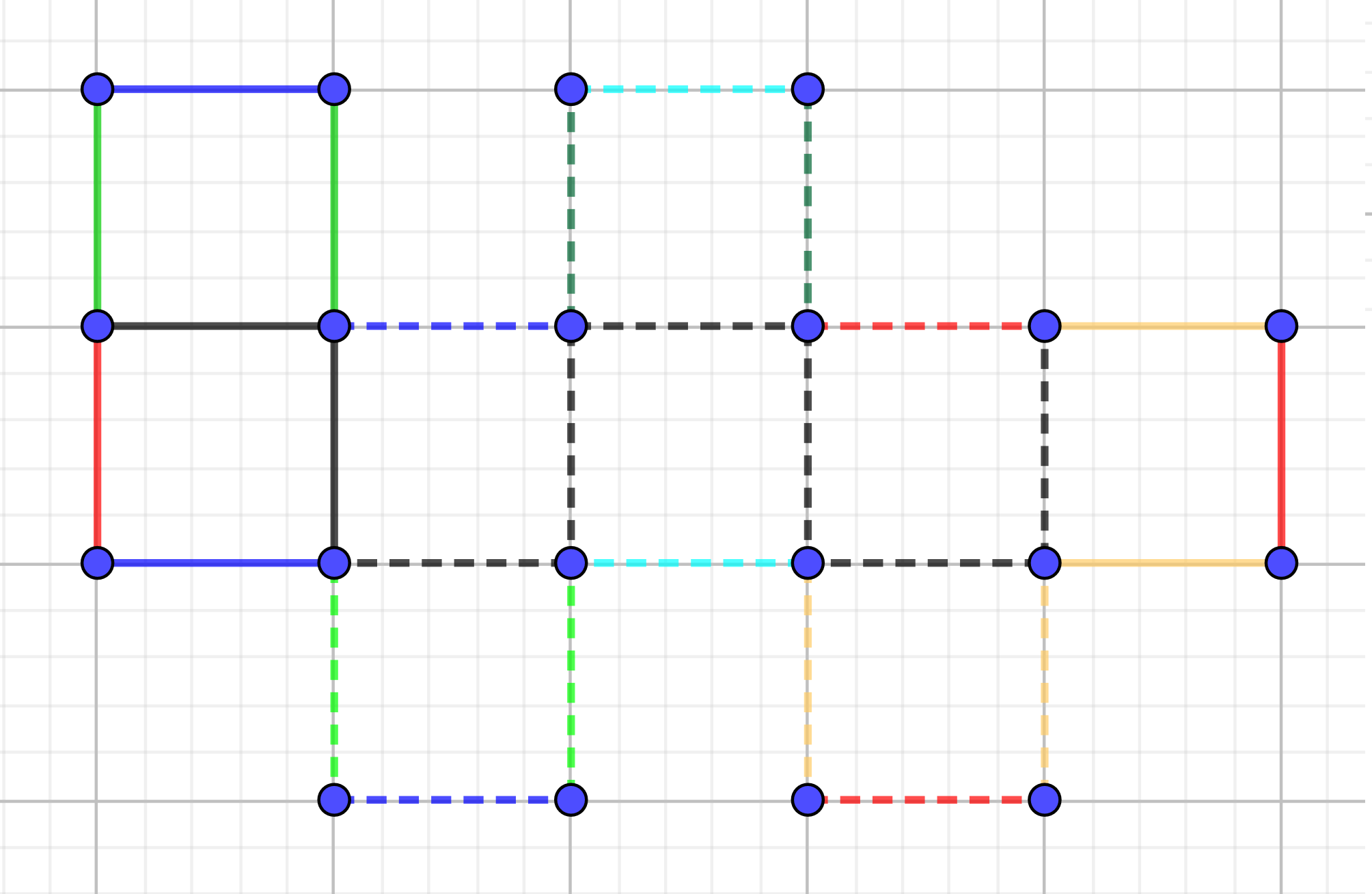
- huit cubes collés entre eux disposés en carré de 3x3 avec un trou à la place du cube du milieu (on peut agrandir autant qu'on veut et faire un carré de 4x4 avec un trou de 2x2 au milieu etc), le tout pavé avec des tuiles carrées
- huit octaèdres disposés de la même manière, arrête contre arrête, avec des tétraèdres pour "boucher" entre les sommets libres des octaèdres, le tout pavé avec des triangles ou des hexagones
- même solution qu'au dessus, mais on sépare le dessus du dessous et on insère des faces rectangulaires entre les deux. Toujours avec un pavage triangulaire ou hexagonal. Dans cette solution, on a inévitablement des tuiles à cheval entre les faces rectangulaires, mais ça reste cohérent.
Voilà le "problème". Il gagnerait sûrement en clarté si il était formulé proprement, avec les bon termes et s'il était illustré. J'en suis désolé.
À défaut d'avoir tout le vocabulaire, si j'ai un peu de temps, je rajouterai des images.
Si vous voyez d'autres solutions, ou d'autres pistes à explorer, je me coucherai moins bête ... mais cela ne m'aidera peut-être pas à trouver le sommeil (c'est terrible quand on pense être sur le point de tenir une solution