Topologie de Zariski

[Finrod]

Ces questions de géométrie algèbrique vous intéressent-t-elles ? (tout se fait à la main)

Soit A un anneau commutatif unitaire. A chaque ouvert (resp fermé) de la topologie de Zariski est associé un idéal qui l'engendre. http://fr.wikipedia.org/wiki/Spectre_premier

On peut démontrer les résultats suivants :

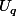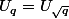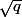1. Si est l'ouvert associé à l'idéal q, alors où est le radical de q.
2. Si deux ouverts sont égaux alors les radicaux de leurs idéaux associés le sont.
3. Si le complémentaire d'un ouvert est un fermé irréductible alors le radical de l'idéal associé à cet ouvert est premier.

[abcd22]

Bonsoir,
Dans la topologie de Zariski on définit les fermés à l'aide d'idéaux, les ouverts sont par définition les complémentaires des fermés, donc je suppose que quand tu parles d'associer un idéal à un ouvert de la topologie de Zariski tu parles d'un idéal associé au complémentaire de l'ouvert. Je trouve plus naturel d'énoncer les propriétés avec des fermés comme elles le sont habituellement, plutôt que d'avoir à passer par des complémentaires.

[Finrod]

Merci abcd22 mais c'est pareil.

Le fermé associé à q est l'ensemble des idéaux premiers contenant q

L'ouvert associé est l'ensemble des idéaux ne contenant pas q


Je fais moi aussi les calculs avec les fermés, mais formellement, les ouverts ne sont pas moins associés aux idéaux que les fermés.

(On a un iso de co-lieu entre les fermé et les idéaux modulo une certaine relation d'équivalence, suggérée d'ailleurs dans l'énoncé ci-dessus.)

ps : un lieu est un ensemble ordonné possédant des sup et des inf plus une propriété de commutativité qui en fait un objet analogue aux ouvert d'un espace topologique.
Un colieu est l'objet dual.
Un lieu n'a pas nécessairement d'espace topologique associé. On parle aussi d'espace topologique sans points.

[abcd22]

À partir d'un fermé F de Zariski on peut trouver facilement un idéal I de A tel que F = V(I), à partir d'un ouvert de Zariski U je ne vois pas de façon de trouver un idéal tel que U = Spec(A)\V(I) sans repasser par les fermés; c'est en ce sens qu'il est plus naturel d'utiliser des fermés.

Je sais bien qu'il est équivalent de parler de fermés ou d'ouverts, d'ailleurs je n'ai pas écrit que ce n'était pas pareil, j'ai dit que ce n'était pas le plus naturel.

[Finrod]

On est d'accord.

En fait il y a une façon naturelle de passer des ouverts aux idéaux mais c'est du niveau recherche.

Cela vient de la théorie des faisceau, si tu connais.

Pour un anneau A, A-mod peut se voir comme la catégorie des préfaisceaux en groupe abélien sur une catégorie possèdant 1 seul objet dont les endomorphismes sont donnés par A. Notons là *A

est ouvert si et seulement si la catégorie B-mod es une sous catégorie de faisceaux en groupe abélien de A-mod.

La théorie des faisceaux (enrichis) nous dit que, à cela on peut faire correspondre un topologie de Grothendieck sur *A qui s'avère être en fait engendré par un idéal de A.