0^0

par **axiome** » 20 Déc 2007, 23:26

Bonjour,
Voilà, mon problème, c'est 0^0. Certains de mes profs de maths disent "fantôme" "n'existe pas". D'autres disent 0^0=0.
Qui a raison ?
Pourriez-vous éclairer ma lanterne ?
Merci d'avance.

par **SimonB** » 20 Déc 2007, 23:40

On pose souvent 0^0=1 pour des simplifications de calcul. Remarque, ça n'a pas grande importance...

par **Lierre Aeripz** » 20 Déc 2007, 23:44

C'est une histoire de convention.

Il est clair que la fonction de deux variables

n'admet pas de limite en zéro, donc on ne peut pas parler de prolongement par continuité.
En revanche, il existe beaucoup de formules portant sur des sommes discrètes (exposant entier) où il est confortable de donner une convention. On choisit généralement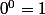

, car c'est souvent la convention qui fait marcher les formules sans exception.
Je dis "généralement" et "souvent" par prudence, mais en fait, je en connais pas d'exemple où l'on choisit la convention

.

par **axiome** » 20 Déc 2007, 23:44

Désolé, je suis impardonnable. Je voulais en effet dire que 0^0=1 et non pas à 0 selon certains de mes profs.

par **axiome** » 20 Déc 2007, 23:45

Oki, merci à tous les deux.

par **bruce.ml** » 21 Déc 2007, 00:30

Salut,

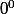, tout comme

pour ne citer que quelques unes des plus connues, sont des formes indéterminées. Si on leur attribue une valeur, cela ne peut être que par convention. Souvent on dit que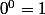

car dans le contexte spécifique dans lequel on est, cette convention aide à ne pas avoir à mettre à part ce cas particulier, comme c'est l'utilité de la plupart des conventions.

par **kazeriahm** » 21 Déc 2007, 02:01

par exemple la suite 0^(1/n) est la suite constante égale à 0 donc tend vers 0 et donc, par convention, on pourrait dire 0^0=0

mais on a x^x=exp(x*ln(x)) qui tend vers 1 quand x tend vers 0 donc 0^0=1

comme déjà dit c'est très conventionnel, et surtout pratique de parler de ce nombre 0^0 qui est une forme indeterminée, alors qu'on ne parle jamais de 0/0, de l'infini mois l'infini, etc...

par **Quidam** » 21 Déc 2007, 12:41

Lierre Aeripz a écrit:Il est clair que la fonction de deux variables n'admet pas de limite en zéro, donc on ne peut pas parler de prolongement par continuité.

Tout à fait d'accord !

En mathématiques, on peut parler des choses que l'on a définies.

Or, a priori,

n'est pas défini !
En général, pour définir une expression, on choisit la continuité. On peut par exemple définir

par :

. Comme

, il est clair que cette limite est égale à 1 !

Mais on peut aussi définir

par :

Pour y non rationnel,

est défini par

lorsque x est strictement positif, mais

ne l'est pas car le logarithme de 0 n'existe pas !
Cependant, si

, avec

et

,

, expression parfaitement définie et égale à 0 !
Alors,

= 0 !

Et puis, varions les plaisirs, on peut aussi chercher :

en choisissant une fonction f qui tend vers 0 lorsque x tend vers 0.
Par exemple, prenons

Ou encore, prenons

!!!

Toutes ces facéties ne sont possibles précisément que parce que, comme l'a dit très justement Lierre Aeripz "la fonction de deux variables

n'admet pas de limite en zéro"

Toutes les définitions possibles sont légales ; une fois définie une expression, on a le droit de l'utiliser ! Mais l'utilisateur est alors tenu de dire quelle définition il choisit : ce ne sera pas une définition universelle !

par **sandrine_guillerme** » 21 Déc 2007, 17:50

Salut à tous,

axiome : mieux vaut un lien qu'un long discours :

:id:

par **sandrine_guillerme** » 21 Déc 2007, 17:52

Salut à tous !

axiome : mieux vaut un lien qu'un long discours :

:id:

par **axiome** » 21 Déc 2007, 18:48

Oki, remerci à tous. Et merci pour le lien Sandrine.
Joyeux Noël.

par **Quidam** » 21 Déc 2007, 20:22

sandrine_guillerme a écrit:Salut à tous !

axiome : mieux vaut un lien qu'un long discours :

:id:

Si tu le dis...

par **Alpha** » 22 Déc 2007, 19:27

sandrine_guillerme a écrit:Salut à tous !

axiome : mieux vaut un lien qu'un long discours :

:id:

Mouais, bof... L'explication de Quidam est très bien selon moi, et son discours, pas si long que ça, nettement plus accessible que celui de la page que tu indiques... Mais bon.

En tout cas merci pour cette réponse Quidam!

Amicalement

par **sandrine_guillerme** » 24 Déc 2007, 03:54

eh ..
sorry ! je n'avais pas du tout lu ce qui était écrit avant au fait !
je parlais pas évidement de QUIDAM, mais de moi même (c'est à dire au lieu que je t'explique ce que j'avais compris axiome dans un long "voir très long discours, je préfère te donner un lien,
mais je n'ai pas du tout lu le posts qui étaient avant,
bref on ne va pas non plus s'étrangler à cause de ça ..

Joyeux Noël QUIDAM joyeux anniversaire et joyeuses pâques aussi si ça te fait penser à quelque chose ! :lol4:

0^0

0^0

Qui est en ligne