Comment a été découvert le nombre Pi ? D'après quel calcul ? J'ai vu un reportage mais j'ai loupé toute la première partie et je sais qu'il y'a eu beaucoup d'approche de pi calculés par tout pleins de civilisations (la plus simple reste 22/7).
Comment a été découvert Pi ? Quelle est le calcul qui permet de trouver ses chiffres suivants?
Pi
8 messages
- Page 1 sur 1
par entropik » 22 Avr 2007, 01:47
Historique du calcul de Pi:
Au XXe siècle av. J.-C. les Babyloniens utilisaient l'approximation 25 / 8 et les Égyptiens ( (16 / 9)2 = 3.16049...) qui était une assez bonne approximation. Ce ne fut qu'au IIIe siècle av. J.-C. qu'une meilleure approximation fut utilisée : vers 250 av. J.-C., grâce à une méthode consistant à encadrer un cercle par deux polygones, Archimède obtint : 223 / 71 <
< 22 / 7 (3.1408... < < 3.1428...), soit 2 décimales exactes.
Au Moyen-Orient en 1429, Al-Kashi calcula 14 décimales de Pi. En 1596, toujours avec des méthodes géométriques, le Hollandais Ludolph van Ceulen calcula 20 décimales, puis 34 en 1609. Il fut si fier de son exploit (il y consacra une bonne partie de sa vie) qu'il demanda à ce que le nombre soit gravé sur sa tombe.
Ensuite, grâce au développement de l'analyse au XVIIe siècle, avec notamment les sommes et produits infinis, le calcul des décimales de Pi s'accéléra. Par exemple, Isaac Newton calcula 16 décimales en 1665, John Machin 100 en 1706. Vers 1760, Euler calcula 20 décimales en une heure (à comparer avec la trentaine de décimales obtenue par Van Ceulen en plus de 10 ans de calcul).
Le mathématicien slovène Jurij Vega calcula en 1789 les 140 premières décimales parmi lesquelles 137 étaient correctes. Ce record tiendra plus de 50 ans. Il améliora la formule que John Machin avait trouvée en 1706 et sa méthode est toujours mentionnée aujourd'hui.
Le mathématicien William Shanks passa 20 ans de sa vie à calculer les décimales de Pi. Il en calcula 707, mais seules les 528 premières étaient correctes. À l'occasion de l'exposition universelle de Paris de 1937, celles-ci furent malheureusement gravées dans la salle du Palais de la Découverte. L'erreur ne fut détectée qu'en 1945.
Le calcul des décimales de Pi s'emballa au XXe siècle avec l'apparition de l'informatique : 2037 sont calculées en 1949 par le calculateur américain ENIAC, 10 000 décimales sont obtenues en 1958, 100 000 en 1961, 1 000 000 en 1973, 10 000 000 en 1982, 100 000 000 en 1989, puis 1 000 000 000 la même année. En 2002, 1 241 100 000 000 décimales étaient connues.
Méthodes de calcul de Pi
Les formules de Machin:
La formule utilisée par John Machin, similaire à des formules encore utilisées aujourd'hui, permet un calcul rapide :
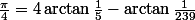
Il l'obtint avec un développement en série de Taylor de la fonction arctan(x). Cette formule peut être vérifiée aisément en coordonnées polaires dans le plan complexe, avec
^4 \times (-239 + i) = -114244 -114244i.)
Les formules de ce genre sont nommées formules de Machin.
Les approximations très précises de sont généralement calculées avec l'algorithme de Gauss-Legendre et l'algorithme de Borwein; l'algorithme de Salamin-Brent, inventé en 1976 a aussi été utilisé pour de très grands nombres de décimales.
On peut voir 1 000 000 de décimales de et de 1/;) sur le Projet Gutenberg (voir liens externes).
Le record actuel est de 1 241 100 000 000 de décimales, déterminées après 600 heures de calcul en novembre 2002 sur un supercalculateur parallèle Hitachi à 64 nuds, avec 1 téraoctet de mémoire centrale, qui pouvait effectuer 2 000 milliards d'opérations en virgule flottante par seconde, soit près de deux fois plus que pour le précédent record (206 milliards de décimales); les formules de Machin suivantes ont été utilisées pour cela :
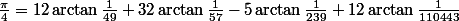(K. Takano, 1982)
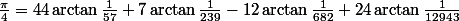(F. C. W. Störmer, 1896)
Ces approximations sont tellement grandes qu'elles n'ont aucune utilisation pratique, si ce n'est tester les nouveaux supercalculateurs.
D'autres méthodes et algorithmes sont actuellement à l'étude et mis en uvre comme l'utilisation en parallèle d'ordinateurs connectés sur le réseau Internet.
Le calcul isolé des décimales de Pi:
En 1995 David Bailey, en collaboration avec Peter Borwein et Simon Plouffe, a découvert une nouvelle formule de, une série (souvent appelée formule BBP):
)
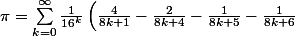Cette formule permet de calculer facilement la ne décimale binaire ou hexadécimale de, sans avoir à calculer les décimales précédentes. Le site de Bailey en contient la dérivation et l'implémentation dans de nombreux langages de programmation. Grâce à une formule dérivée de la formule BBP, le 4 000 000 000 000 000e chiffre de en base 2 a été obtenu en 2001.
Un an plus tard, Simon Plouffe met au point un algorithme permettant le calcul de la ne décimale de, mais cette fois-ci en décimal. Il est décrit dans un court article disponible depuis la page de Simon Plouffe (http://www.lacim.uqam.ca/~plouffe/Simon/articlepi.html). Malheureusement, cet algorithme qui permet actuellement de déterminer en base 10 un chiffre précis et isolé de est moins rapide que celui qui consiste à calculer tous les chiffres décimaux précédents.
Autres formules:
D'autres formules ont été utilisées pour calculer dont:
!(1103+26390k)}{(k!)^4 396^{4k}})
(formule due à Ramanujan<br /><br /><br /><br /><br /><br /> \frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}})
(formule due à David et Gregory Chudnovsky)
Au XXe siècle av. J.-C. les Babyloniens utilisaient l'approximation 25 / 8 et les Égyptiens ( (16 / 9)2 = 3.16049...) qui était une assez bonne approximation. Ce ne fut qu'au IIIe siècle av. J.-C. qu'une meilleure approximation fut utilisée : vers 250 av. J.-C., grâce à une méthode consistant à encadrer un cercle par deux polygones, Archimède obtint : 223 / 71 <
< 22 / 7 (3.1408... < < 3.1428...), soit 2 décimales exactes.Au Moyen-Orient en 1429, Al-Kashi calcula 14 décimales de Pi. En 1596, toujours avec des méthodes géométriques, le Hollandais Ludolph van Ceulen calcula 20 décimales, puis 34 en 1609. Il fut si fier de son exploit (il y consacra une bonne partie de sa vie) qu'il demanda à ce que le nombre soit gravé sur sa tombe.
Ensuite, grâce au développement de l'analyse au XVIIe siècle, avec notamment les sommes et produits infinis, le calcul des décimales de Pi s'accéléra. Par exemple, Isaac Newton calcula 16 décimales en 1665, John Machin 100 en 1706. Vers 1760, Euler calcula 20 décimales en une heure (à comparer avec la trentaine de décimales obtenue par Van Ceulen en plus de 10 ans de calcul).
Le mathématicien slovène Jurij Vega calcula en 1789 les 140 premières décimales
parmi lesquelles 137 étaient correctes. Ce record tiendra plus de 50 ans. Il améliora la formule que John Machin avait trouvée en 1706 et sa méthode est toujours mentionnée aujourd'hui.Le mathématicien William Shanks passa 20 ans de sa vie à calculer les décimales de Pi. Il en calcula 707, mais seules les 528 premières étaient correctes. À l'occasion de l'exposition universelle de Paris de 1937, celles-ci furent malheureusement gravées dans la salle
du Palais de la Découverte. L'erreur ne fut détectée qu'en 1945.Le calcul des décimales de Pi s'emballa au XXe siècle avec l'apparition de l'informatique : 2037 sont calculées en 1949 par le calculateur américain ENIAC, 10 000 décimales sont obtenues en 1958, 100 000 en 1961, 1 000 000 en 1973, 10 000 000 en 1982, 100 000 000 en 1989, puis 1 000 000 000 la même année. En 2002, 1 241 100 000 000 décimales étaient connues.
Méthodes de calcul de Pi
Les formules de Machin:
La formule utilisée par John Machin, similaire à des formules encore utilisées aujourd'hui, permet un calcul rapide :
Il l'obtint avec un développement en série de Taylor de la fonction arctan(x). Cette formule peut être vérifiée aisément en coordonnées polaires dans le plan complexe, avec
Les formules de ce genre sont nommées formules de Machin.
Les approximations très précises de
sont généralement calculées avec l'algorithme de Gauss-Legendre et l'algorithme de Borwein; l'algorithme de Salamin-Brent, inventé en 1976 a aussi été utilisé pour de très grands nombres de décimales.On peut voir 1 000 000 de décimales de
et de 1/;) sur le Projet Gutenberg (voir liens externes).Le record actuel est de 1 241 100 000 000 de décimales, déterminées après 600 heures de calcul en novembre 2002 sur un supercalculateur parallèle Hitachi à 64 nuds, avec 1 téraoctet de mémoire centrale, qui pouvait effectuer 2 000 milliards d'opérations en virgule flottante par seconde, soit près de deux fois plus que pour le précédent record (206 milliards de décimales); les formules de Machin suivantes ont été utilisées pour cela :
Ces approximations sont tellement grandes qu'elles n'ont aucune utilisation pratique, si ce n'est tester les nouveaux supercalculateurs.
D'autres méthodes et algorithmes sont actuellement à l'étude et mis en uvre comme l'utilisation en parallèle d'ordinateurs connectés sur le réseau Internet.
Le calcul isolé des décimales de Pi:
En 1995 David Bailey, en collaboration avec Peter Borwein et Simon Plouffe, a découvert une nouvelle formule de
, une série (souvent appelée formule BBP):Cette formule permet de calculer facilement la ne décimale binaire ou hexadécimale de
, sans avoir à calculer les décimales précédentes. Le site de Bailey en contient la dérivation et l'implémentation dans de nombreux langages de programmation. Grâce à une formule dérivée de la formule BBP, le 4 000 000 000 000 000e chiffre de en base 2 a été obtenu en 2001.Un an plus tard, Simon Plouffe met au point un algorithme permettant le calcul de la ne décimale de
, mais cette fois-ci en décimal. Il est décrit dans un court article disponible depuis la page de Simon Plouffe (http://www.lacim.uqam.ca/~plouffe/Simon/articlepi.html). Malheureusement, cet algorithme qui permet actuellement de déterminer en base 10 un chiffre précis et isolé de est moins rapide que celui qui consiste à calculer tous les chiffres décimaux précédents.Autres formules:
D'autres formules ont été utilisées pour calculer
dont:par cesar » 22 Avr 2007, 06:59
question : y a t il un interet à calculer un aussi grand nombre de décimales ?
en maths on manipule pi sous forme de son symbole et non pas sous forme de chiffre... On sait que le nombre de décimales de pi est infini, quel besoin a t on de les connaitre au dela des premieres qui sont necessaires au niveau pratique ?
en maths on manipule pi sous forme de son symbole et non pas sous forme de chiffre... On sait que le nombre de décimales de pi est infini, quel besoin a t on de les connaitre au dela des premieres qui sont necessaires au niveau pratique ?
par entropik » 22 Avr 2007, 13:31
cesar a écrit:question : y a t il un interet à calculer un aussi grand nombre de décimales ?
A mon avis le seul intérêt est de posséder le record de celui qui a trouvé le plus de décimales.
cesar a écrit:en maths on manipule pi sous forme de son symbole et non pas sous forme de chiffre... On sait que le nombre de décimales de pi est infini, quel besoin a t on de les connaitre au dela des premieres qui sont necessaires au niveau pratique ?
Il n'y a que les ingénieurs qui en ont besoin dans leurs calculs finaux dirait-on. Maintenant cette précision est-elle bien nécessaire?
"Pour l'utilisation courante, 3,14 ou 22/7 sont souvent suffisants, bien que les ingénieurs utilisent plus souvent 3,1416 (5 chiffres significatifs) ou 3,14159 (6 chiffres significatifs) pour plus de précision dans leurs calculs préliminaires (dans les calculs finaux, cependant, ils doivent utiliser la précision maximale de l'ordinateur, soit de 8 à 19 chiffres significatifs)."
par Dominique Lefebvre » 22 Avr 2007, 14:46
cesar a écrit:question : y a t il un interet à calculer un aussi grand nombre de décimales ?
en maths on manipule pi sous forme de son symbole et non pas sous forme de chiffre... On sait que le nombre de décimales de pi est infini, quel besoin a t on de les connaitre au dela des premieres qui sont necessaires au niveau pratique ?
Oui, c'est vrai, quel intérêt? Quel intérêt de se poser des questions sur la fermeture de l'univers, sur les premières picosecondes du big bang ou sur les ensembles de Cantor...
Tout simplement pour savoir!
Et aussi pour certaines utilisations pratiques. Par exemple, existe-t-il des séquences répétitives dans la suite décimale de pi ? La réponse peut être utile en crypto...
Peut-on définir une fonction de densité sur les premiers dans la séquence décimale: utile pour les matheux...
Et d'autres aussi!
Alors, oui bien sur il y a un intérêt à étudier la séquence décimale de PI.
par entropik » 22 Avr 2007, 16:06
Dominique Lefebvre a écrit:Oui, c'est vrai, quel intérêt? Quel intérêt de se poser des questions sur la fermeture de l'univers, sur les premières picosecondes du big bang ou sur les ensembles de Cantor...
Tout simplement pour savoir!
Je pense que ça ne se limite pas à combler l'envie de savoir, cela permet à l'homme de s'enivrer de connaissances et d'éveiller la jubilation. Il faudrait célébrer les découvertes et les créations comme autant de révélations des merveilleuses potentialités de la matière primordiale. Des voies nouvelles s'ouvrent pour transformer les moments de notre existence en instants d'exultation.
par cesar » 22 Avr 2007, 16:09
Dominique Lefebvre a écrit:Et aussi pour certaines utilisations pratiques. Par exemple, existe-t-il des séquences répétitives dans la suite décimale de pi ? La réponse peut être utile en crypto...
Peut-on définir une fonction de densité sur les premiers dans la séquence décimale: utile pour les matheux...
Et d'autres aussi!
Alors, oui bien sur il y a un intérêt à étudier la séquence décimale de PI.
vous avez mal saisi ma question ou bien je l'ai pas bien formulée: il y a des tas de nombre du meme genre : e par exemple, et d'autres constantes. Les raisons que vous donnez pour calculer pi peuvent aussi bien s'appliquer à eux aussi... or les calcule t on ???
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :