X² - x - 1 = 0 ?
50 messages
- Page 3 sur 3 - 1, 2, 3
Non tu n'as pas le niveau pour le factoriser et tu n'as pas le temps non plus (remarque: moi non plus je n'ai ni le niveau pour obtenir un truc plus ou moins propre, ni le temps :we: )
Bon en fait pour factoriser un polynôme il faut connaitre ses racines... et pour connaitre les racines d'un polynôme de degré 2, on peut utiliser le discriminant.
L'histoire avec les racines est importante:
Si tu as une racine d'un polynôme , alors tu peux mettre
une racine d'un polynôme , alors tu peux mettre ) en facteur dans le polynôme.
en facteur dans le polynôme.
Comme tu parles de C:
On montre dans C, mais c'est très délicat et tu n'as peut être pas les outils pour comprendre la demo, que tout polynôme de degré 1 est scindé c'est à dire qu'on peut l'écrire comme produit de polynômes de degré 1.
1 est scindé c'est à dire qu'on peut l'écrire comme produit de polynômes de degré 1.
Si on veut se ramener dans R, le problème c'est qu'il y a surement des complexes dans la "factorisation".
Le truc c'est que les polynomes du 1er degré "complexes" dans notre factorisation vont par paires: en multipliant les paires entre elles, on tombe sur un polynôme de degré 2 ( logique...) mais qui est réel (enfin à coefficients réels) .
Le plus notable c'est que le polynôme final, vu qu'on connait sa factorisation qui est "complexe", on peut affirmer qu'on ne peut pas plus le factoriser dans R (il y a une histoire d'unicité là dessous)...
ça doit te paraitre un peut obscure donc un exemple est bienvenu.
On prend le polynôme:

Ce polynôme n'admet pas de racines dans R (tu peux vérifier, en posant X=x^2, tu tombera sur un polynôme de degré 2 en X).
Je t'affirme (tu peux vérifier) que ses racines complexes sont:
i,-i, 2i,-2i.
Le polynôme se factorise donc comme suit:(x-i)(x+i)(x-2i)(x+2i)
Comme tu l'as certainement intuité, les "paires " sont ici:
(x-i) et(x+i), suivis de (x-2i)et(x+2i).
Donc en développant:
(x+i)=x^2+1) et
et (x+2i)=x^2+4) (remarque qu'on tombe bien sur des trucs "réels"
(remarque qu'on tombe bien sur des trucs "réels"
On obtient donc la factorisation dans R:
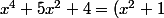(x^2+4))
Bon en fait pour factoriser un polynôme il faut connaitre ses racines... et pour connaitre les racines d'un polynôme de degré 2, on peut utiliser le discriminant.
L'histoire avec les racines est importante:
Si tu as
Pourquoi?
J'ai lu ça quelque part, mais je ne vois pas pourquoi.
Comme tu parles de C:
On montre dans C, mais c'est très délicat et tu n'as peut être pas les outils pour comprendre la demo, que tout polynôme de degré
Si on veut se ramener dans R, le problème c'est qu'il y a surement des complexes dans la "factorisation".
Le truc c'est que les polynomes du 1er degré "complexes" dans notre factorisation vont par paires: en multipliant les paires entre elles, on tombe sur un polynôme de degré 2 ( logique...) mais qui est réel (enfin à coefficients réels) .
Le plus notable c'est que le polynôme final, vu qu'on connait sa factorisation qui est "complexe", on peut affirmer qu'on ne peut pas plus le factoriser dans R (il y a une histoire d'unicité là dessous)...
ça doit te paraitre un peut obscure donc un exemple est bienvenu.
On prend le polynôme:
Ce polynôme n'admet pas de racines dans R (tu peux vérifier, en posant X=x^2, tu tombera sur un polynôme de degré 2 en X).
Je t'affirme (tu peux vérifier) que ses racines complexes sont:
i,-i, 2i,-2i.
Le polynôme se factorise donc comme suit:(x-i)(x+i)(x-2i)(x+2i)
Comme tu l'as certainement intuité, les "paires " sont ici:
(x-i) et(x+i), suivis de (x-2i)et(x+2i).
Donc en développant:
On obtient donc la factorisation dans R:
Le_chat a écrit:
On prend le polynôme:
Ce polynôme n'admet pas de racines dans R (tu peux vérifier, en posant X=x^2, tu tombera sur un polynôme de degré 2 en X).
Je t'affirme (tu peux vérifier) que ses racines complexes sont:
i,-i, 2i,-2i.
Le polynôme se factorise donc comme suit:(x-i)(x+i)(x-2i)(x+2i)
Comme tu l'as certainement intuité, les "paires " sont ici:
(x-i) et(x+i), suivis de (x-2i)et(x+2i).
Donc en développant:et
(remarque qu'on tombe bien sur des trucs "réels"
On obtient donc la factorisation dans R:
Commençons par l'exemple mdr, puisque je ne vois pas TROP :mur: :triste: Désolé..!
En fait:
Non? :hein:
Tu t'es peut-être trompé quelque part?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
50 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
