Théorème existant sur 3 nombres premiers consécutifs ?

[Baptiste789]

Bonsoir,
j'aimerais savoir s'il existe déjà un théorème ou alors comment démontrer que si nous prenons 3 nombres premiers de rang consécutif la somme des deux plus petits nombres premiers est plus grand que le 3ème.
Par exemple prenons 3, 5 et 7:
3+5>7
J'aimerais aussi qu'on enlève le cas particulier 2 3 et 5 à l'énoncé.
Merci d'avance pour votre réponse.

[Rdvn]

Bonsoir

Le résultat est confirmé sur :
Jean-Paul Delahaye
Merveilleux nombres premiers
BELIN POUR LA SCIENCE
page 213

mais sans démonstration (dont on se doute qu'elle n'est probablement pas facile)
Bonne lecture

[Ben314]

Salut,
En utilisant les gros outils, à savoir le fait que et les constantes effective qu'on connait concernant cet équivalent, le résultat devient évident.
A la limite, on peut noter que le résultat peut s'exprimer sous la forme :
Etant donné deux nombre premier successifs , il y a au moins un nombre premier strictement compris entre et .
Ce qui est un peu plus fort (mais pas des masse) que ce qui est, à mon sens, l'un des premier résultat non triviaux sur la répartition des nombres premiers : le postulat de Bertrand , à savoir que, pour tout entier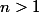 il y a au moins un nombre premier entre et (une des preuves de ce résultat, à savoir celle donnée sur Wiki. n'utilise que des outils élémentaires).

[Rdvn]

Bonsoir
C'est intéressant, mais effectivement ce sont de "gros outils" .
Trouve-t-on de la documentation (sur le net) sur les constantes adéquates ?
Bonne soirée

[Ben314]

Dans la page de wiki dédiée, tu as des majorations explicites : (voire plus précis en supposant l'hypothèse de Riemann vérifiée).

[Rdvn]

Merci
Bonne journée