Bonjour!
Inspiré par le test de Lucas-Lehmer pour les nombres de Mersenne, j’ai formulé l’affirmation suivante :
Soit
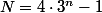
où
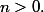
Soit
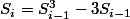
avec
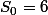
. Alors

est premier si et seulement si

.
Vous pouvez faire ce test
ici.
Preuve de la suffisance.J’ai essayé d’imiter la preuve de Bruce du test de Lucas-Lehmer. Laissez
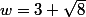
et
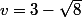
. Il est alors possible de montrer (par induction) que
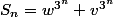
. Donc

divise
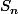
signifie qu’il y a un entier

tel que
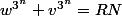
.Multiplié par
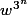
donne

La quadrature des deux côtés de cette égalité donne
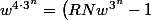^2 \tag{2})
Pour preuve par contradiction, supposons que

est composé et choisissez un de ses diviseurs premiers

qui n’est pas supérieur à sa racine carrée. Considérons le groupe
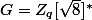
de tous les nombres
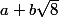
modulo

qui sont inversables. Le groupe

a au plus des éléments
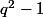
. En affichant

modulo

, les égalités (1) et (2) ci-dessus deviennent

et

.
Nous avons donc montré que l’ordre de

divise
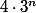
. Afin de compléter la preuve, nous devons montrer que
)
est exactement
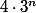
mais je ne vois pas pourquoi cela devrait être le cas. Est-il possible de montrer que
 =4 \cdot 3^{n})
? Est-il possible de prouver la suffisance de la revendication par une autre méthode?
