Tables et rencontres

[Braun]

Bonjour,

Je souhaiterais solutionner un problème d'organisation. J'envisage de convier
81 personnes à des rencontres professionnelles et faire en sorte que chaque participant
se rencontre une fois.

Je disposerai de 9 tables disposant chacune de 9 chaises ainsi chaque personnes se présente à 8 autres.
Un fois le tour de table effectué, les participants changent de table.
En 10 séquences, tous les participants auront rencontré les 80 autres !

Comment affecter les participants à chaque table et à chaque séquence !?

Merci de votre aide

BM

[Ben314]

Salut,
Je pense que le principe marche à tout les coups, mais c'est à vérifier...

S'il y a 3x3 participants numérotés de 0 à 8 (et oui, je suis matheux...) et 3 tables de 3, on fait :



La "logique" de la séquence 1 est évidente. Pour toutes les autres séquences, on commence par mettre sur dans les tables 1,2 et 3 les personnes 0,1,2

Pour la séquence 2, on ajoute aux tables 1,2,3 les personnes 3,4,5 (dans cet ordre) puis on ajoute aux tables 1,2,3 les personnes 6,7,8 (dans cet ordre).

Pour la séquence 3, on ajoute aux tables 1,2,3 les personnes 3,4,5 (décalés d'un cran) puis on réajoute aux tables 1,2,3 les personnes 6,7,8 (décalés de deux crans).

Pour la séquence 4, on ajoute aux tables 1,2,3 les personnes 3,4,5 (décalés de deux crans) puis on réajoute aux tables 1,2,3 les personnes 6,7,8 (décalés de 4 crans, c'est à dire d'un cran).

Le seul truc dont je soit pas trop certain, c'est de savoir si ça marche dans le cas général de n² personnes et pas uniquement dans le cas où n est premier (et hélas 9 n'est pas premier... :hum:)

[Ben314]

Effectivement, la méthode çi dessus ne marche que si est premier.
Si on regarde les personnes comme des couples , la méthode en question consiste à :

A la séquence 1, on met à la table les tels que

Les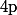 autres séquences correspondent aux différents et, lors de cette séquence, on met à la table les tels que

Deux personnes distinctes vont effectivement se rencontrer une et une seule fois vu que par deux points distincts de il passe une et une seule droite.

Sauf que... ça marche pas pour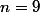 qui n'est pas premier...
Et je conjecturerais bien (un peu au pif...) que ça va pas être faisable.

[Ben314]

Ben si, c'est faisable...
Car 9 n'est pas premier, mais c'est une puissance d'un nombre premier donc il existe un corps à 9 éléments et il suffit de faire la même chose que çi dessus dans ce corps là...

[Braun]

Ben si, c'est faisable...
Car 9 n'est pas premier, mais c'est une puissance d'un nombre premier donc il existe un corps à 9 éléments et il suffit de faire la même chose que çi dessus dans ce corps là...

Salut,

Merci, je vais essayer de reproduire les séquences avec 9 par tables comme indiqué !

Bonne soirée

BM

[Ben314]

Avec 9 par tables, ça va être plus compliqué que simplement "de faire tourner" vu que ce qu'on va manipuler, c'est effectivement des "équations de droites" de la forme y=ax+b, mais a,b,x et y font être des trucs de la forme u+iv où u et v sont des éléments de Z/3Z et i²=-1 donc les "décalages" ne vont pas se résumer à de bêtes permutations circulaires.

Je te fait un truc sous OpenOffice (Tableur)

d'ici une petite 1/2 heure je pense...

[Ben314]

https://drive.google.com/file/d/0ByyHQqLyqzSuS0ZLS29EMkhwcDQ/view?usp=sharing

[Mathusalem]

Salut,

Je profite de ce fil, car le problème est très similaire à un problème d'organisation que j'ai.

Dans mon cas, j'aurais (p.ex) 12 personnes à répartir sur 4 tables de 3 personnes. En reprenant tes notations, je regarde mes 12 personnes comme des couples .

Le nombre d'étape est une variable. J'obtiens très vite des doublons (personne i et j déjà vus auparavant), car dans ce cas il n'y a pas qu'une et une seule droite passant par deux points distincts de (ce qui tient au fait que 4 n'est pas premier?). Ma contrainte n'est pas que tout le monde ne se voie qu'une fois, mais pour un nombre d'étapes fixes, d'étaler les personnes le mieux possible (minimiser la mesure , avec = nb de fois que personne i et j se sont vues).

Est-ce que tu penses qu'il y a une méthode pour construire des 'tables', c'est-à-dire un ordre dans lequel traverser les parametres de la droite, pour optimiser la répartition des rencontres ?

PS: Pour ce cas, à la 5ème étape, il est impossible d'éviter des paires qui se rencontrent deux fois. C'est possible uniquement jusqu'à 4 étapes. Pour 15 personnes à répartir sur 5 tables de 3, impossible d'éviter les doubles dès la 6è étape. Est-ce que cela tient au fait que 12 = [3]x4, 15 = [3]x5 ?

[Ben314]

J'ai pas la réponse (et je ne suis pas persuadé qu'il y en ait une de simple).

De tout façon, dés le départ, si on cherche à voir le problème par de la "géométrie" il y a un problème : comment définir une "droite" sur un truc qui n'est pas un k-espace vectoriel :
Si on la définit par du y=ax+b ou autre ax+by+c=0, on ne voit pas bien où sont sensé "vivre" les coeff. des équations pour que ça ait du sens (x est dans Z/3Z et ax est sensé être dans Z/4Z...)
A la limite, on peut les définir par des équation paramétriques x=xo+at et y=yo+bt où t est en fait un entier (donc on peut le voir soit comme un élément de Z/3Z, soit comme un élément de Z/4Z), mais je ne sait pas si ça a un quelconque intérêt dans l'optique de ton problème vu que les droites n'auront pas toute le même nombre d'éléments (il y aura par exemple des droites égales à l'espace tout entier...)

[Braun]

Bonsoir,

Effectivement j'obtiens des doublons dés la 4 eme ou 5 eme séquence ! :(

Je me disais qu'il faudrait peut etre traiter les groupes en augmentant le nombre de participants par tables ?!

BM

[Braun]

Bonsoir,

je vais regarder cette table attentivement elle semble complexe !

Merci

BM