Système du second ordre
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 20 Mai 2014, 12:56
par Macflurry » 20 Mai 2014, 12:56
Bonjour,
J'aimerais pouvoir approximer la courbe ci dessous par un système du second ordre avec une entrée impulsionnelle:
 imagik
imagikLe soucis est que je n'arrive pas à déterminer les coefficients d'amortissement, et sa pulsation propre.
Pouvais vous m'indiquer la marche à suivre?
voici la courbe que j'aimerais prendre comme modèle de modélisation :
http://www-hadoc.lag.ensieg.inpg.fr/hadoc/continu/n04/r04-05.htmToute aide est la bienvenue.
Nicolas
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 20 Mai 2014, 14:37
par Cliffe » 20 Mai 2014, 14:37
[CENTER]

[/CENTER]
On a besoin des valeurs en abscisse.
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 20 Mai 2014, 14:48
par Macflurry » 20 Mai 2014, 14:48
Cliffe a écrit:[CENTER]

[/CENTER]
On a besoin des valeurs en abscisse.
voici les abscisse :
 imagik
imagikSi vous pouviez me donner les calculs pour que je puisse le faire par moi même pour la suite .
Merci a toi Cliffe
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 20 Mai 2014, 14:51
par Cliffe » 20 Mai 2014, 14:51
La courbe avec les abscisses :s
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 20 Mai 2014, 14:58
par Macflurry » 20 Mai 2014, 14:58
Cliffe a écrit:La courbe avec les abscisses :s
Désolé je n'avais pas fait attention
Voila
 imagik
imagik
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 20 Mai 2014, 15:20
par Cliffe » 20 Mai 2014, 15:20
Je voulais voir les deux sur le mm graphique.
[CENTER]
 + 2z\omega_0\frac{dt}{dt}s(t)+\omega_0^2s(t)=K\omega_0^2)
[/CENTER]
Tu obtiens le K en prenant t = infiny.
Le z avec le premier dépassement.
Le w0 avec la "distance" entre deux pics.
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 20 Mai 2014, 15:23
par Macflurry » 20 Mai 2014, 15:23
Cliffe a écrit:Je voulais voir les deux sur le mm graphique.
[CENTER]
 + 2z\omega_0\frac{dt}{dt}s(t)+\omega_0^2s(t)=K)
[/CENTER]
Tu obtiens le K en prenant t = infiny.
Le z avec le premier dépassement.
Le w0 avec la "distance" entre deux pics.
Merci mais sur mon graphique je n'ai pas deux pics, c'est le soucis non?
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 20 Mai 2014, 15:34
par Cliffe » 20 Mai 2014, 15:34
[CENTER]

[/CENTER]
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 20 Mai 2014, 15:46
par Macflurry » 20 Mai 2014, 15:46
Cliffe a écrit:[CENTER]

[/CENTER]
je tavouerais etre un peu perdu.... :mur:
Je sais que ce n'est pas bien compliqué mais je n'y arrive pas
K=380
mais aprés je galère
le w0= 2*PI/le temps entre deux pics je trouve 17.14 environ
et le dépassement reste un mystere
Peut tu me le détailler s'il te plait.?
Je t'en serais reconnaissant :hum:
PS: Le temps de réponse n'est n'influe pas sur le calcul?
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 20 Mai 2014, 16:13
par Cliffe » 20 Mai 2014, 16:13
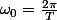
Premier dépassement :
[CENTER]
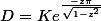
[/CENTER]
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 20 Mai 2014, 16:27
par Cliffe » 20 Mai 2014, 16:27
Que pense tu de ça :
[CENTER]

[/CENTER]
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 21 Mai 2014, 17:04
par Macflurry » 21 Mai 2014, 17:04
Merci beaucoup :p
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 21 Mai 2014, 17:07
par Cliffe » 21 Mai 2014, 17:07
Mon modèle ne fonctionne que si la dérivée est nul en 0 ...
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 22 Mai 2014, 08:13
par Macflurry » 22 Mai 2014, 08:13
Juste une petite précision concernant l'amortissement peut tu m'indiquer comment tu trouve le Z.
Je suis bloqué, désolé de ma nullité en math... :marteau:
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 22 Mai 2014, 09:41
par Cliffe » 22 Mai 2014, 09:41
Tu étudies quel système exactement ? Un circuit électrique ? C'est de la physique ?
Pour le dépassement, on a D = 10 :
[CENTER]
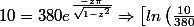 \right ]^2 \left ( 1-z^2 \right ) = z^2\pi^2 \Rightarrow z^2 \left ( \pi^2 + \left [ln\left ( \frac{10}{380} \right ) \right ]^2 \right ) = \left [ln\left ( \frac{10}{380} \right ) \right ]^2 \Rightarrow z = - \frac{ln \left ( \frac{10}{380} \right )} {\sqrt{\pi^2 + \left [ln\left ( \frac{10}{380} \right ) \right ] ^2 }} \approx 0.75681879)
[/CENTER]
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 23 Mai 2014, 08:15
par Macflurry » 23 Mai 2014, 08:15
Merci beaucoup de ton aide, j'essaye de reproduire des systemes en les simplifiant par la modélisation.
Une autre é***** si tu veux bien continuer à m'aider :hum:

J'ai pensé à l'opérateur sigmoide mais la courbe n'est pas symétrique au niveau du point d'inflection ..
Si tu as une idée je suis preneur.
Je te remercie encore de ton aide
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 23 Mai 2014, 09:52
par Cliffe » 23 Mai 2014, 09:52
ça resemble à une courbe de pH en phyisque.
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 03 Juin 2014, 09:18
par Macflurry » 03 Juin 2014, 09:18
Je reviens à la charge avec une nouvelle courbe à modéliser:
[url=http://imagik.fr/view/101391]

Je pensais la modéliser par un premier ordre mais encore mes lacunes en math me font défauts.
Si vous pouviais m'aider.
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 03 Juin 2014, 10:35
par Cliffe » 03 Juin 2014, 10:35
Y'a plusieurs manières de modéliser tes courbes ...
[CENTER]


[/CENTER]
-
Macflurry
- Membre Naturel
- Messages: 11
- Enregistré le: 20 Mai 2014, 12:46
-
 par Macflurry » 03 Juin 2014, 10:46
par Macflurry » 03 Juin 2014, 10:46
J'aimerais concaténer une constante et apres un premier ordre mais si tu as une autre idée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
 imagik
imagik
 [/CENTER]
[/CENTER]

 [/CENTER]
[/CENTER] [/CENTER]
[/CENTER]


 [/CENTER]
[/CENTER]