Sur le modèle de l'équation de Pell Fermat

[anthony_unac]

Bonjour,

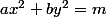
Sachant que l'équation de Pell Fermat est résoluble (notamment à l'aide d'un algorithme), existe t il de la même manière des méthodes de résolution pour l'équation (plus générale) diophantienne ou la solution recherchée sont tous les couples d'entiers pour , et trois entiers donnés ?

PS: On peut encore généraliser et se poser la question pour toutes les équations de la forme
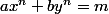
A ma connaissance le cas n=1 est bien connu mais pour le reste ??

[nodgim]

a,b,m entiers naturels ou relatifs ?

[anthony_unac]

On peut se poser la question de savoir s'il existe des méthodes de résolution dans les deux cas (naturels et relatifs). J'imagine que des méthodes numériques de résolution ont déjà vu pointer le bout de leur nez mais qu'en est il réellement ?

[nodgim]

Ce n'est pas du tout la même approche avec des entiers naturels ou relatifs. Avec des entiers naturels, le nombre de solutions est fini. D'où ma question, pas vraiment anecdotique.

[anthony_unac]

Avec des entiers naturels, le nombre de solutions est fini. D'où ma question, pas vraiment anecdotique.

Pour le cas n=1, il n'y a une infinité de couples d'entiers solution qu'on se place dans N ou dans Z non ?

[nodgim]

Dans l'équation ax² - by² = + ou - m, les solutions, quand elles existent, sont en nombre infini. Quand on en a 2, on les a toutes. L'arithmétique qui se cache derrière doit être ardue, je ne la connais pas. C'est seulement en faisant qq essais qu'on se rend compte à peu près comment ça marche.