Suite de Syracuse.

[mathelot]

Bonjour,

je me demande , pour valeurs initiales de l'intervalle
si la "phase horizontale" ne prend pas fin dans un voisinage de la n-ième itérée (pour k=n).

[mathelot]

Bonjour,

i)
Dans le dernier graphique, on transforme l'exponentielle décroissante
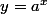
en , avec une pente ln(a) négative.

Peux tu calculer cette pente ? est-ce ln(2)-ln(3) ?

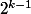
ii) je reviens sur la description des suites arithmétiques au rang k (k=nombre d'itérées) : cette description met de l'ordre dans le chaos Collatz en décrivant ce qui se passe au niveau des orbites de façon transverse (en coupe), mais ne règle pas le problème.
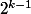
En effet, les suites arithmétiques ont besoin de "valeurs initiales" et le chaos resurgit où on ne l'attendait pas, pour la loi d'apparition des "valeurs initiales" de chaque suite arithmétique.

iii)
autre aspect intriguant: l'arbre binaire, basé sur la dichotomie 1/2,3/2
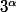
, lors de chaque itération k=k+1, partitionne la suite arithmétique de raison en deux suites arithmétiques, un terme sur deux pair, un terme sur deux impair, vû que la raison en est un entier naturel impair.

Cet algorithme a des similitudes avec l'opérateur FFT (Fast Fourier Transform ou transformée de Fourier binaire discrète).
ici
L'idée serait d'associer, au vecteur de taille
des valeurs initiales, sa transformée de Fourier discrète en espérant suivre les orbites par l'opérateur de Fourier F, si une formule pour existe
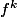
( étant le -uplet , vecteur à coordonnées entières, de taille résultant de la k-ième itérée de Collatz sur chaque coordonnée)

là

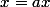
j'ai regardé hier les formules de l'opérateur de Fourier, certaines concernent les dilations et d'autres les translations

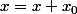et là
à suivre...

olivier