Bonjour,
C'est bien connu, les valeurs initiales
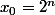
donnent des chaines (descendantes) de longueur arbitraire, ce qui l'est moins,c'est que les valeurs initiales
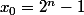
et
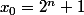
donnent des vols
en altitude arbitrairement longs;
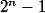
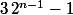
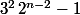
...
on note aussi que des entiers naturels en progression arithmétique de raison
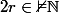
)
ont des images par Collatz en progression arithmétique de raison

ou
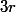
selon la parité du 1er terme

à cause de l'aspect affine des applications
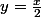
et
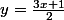
je m'interroge de savoir si l'on peut associer à un intervalle
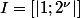
de "valeurs initiales" un algorithme papillon style FFT (fast fourier transform)
de dichotomie sur un arbre binaire dont les noeuds sont constitués de suites arithmétiques, la moitié des valeurs, supposées en progression arithmétique de raison

ont des images plus haut en progression arithmétique de raison
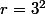
,
la moitié des valeurs en progression arithmétique de raison r=3
ont des images plus bas en progression arithmétique de raison

On peut se demander également si la durée des vols ne serait pas répartie comme une "
http://fr.wikipedia.org/wiki/Planche_de_Galton "
à cause de la dichotomie 1/2 ;3/2 , planche de Galton infinie pour l'ensemble des valeurs initiales

, ce qui fait que les courbes en cloche de la planche de Galton sont masquées
et peu visibles de façon immédiate à moins de faire tourner l'algorithme de dichotomie sur les
suites arithmétiques (leur nombre double à chaque itération)
exemple: ensemble de valeurs initiales [|1;16|] en progression arithmétique de raison r=1
un terme sur deux est pair, un terme sur deux est impair
Par Collatz (nombre d'itérées k=1)
ça donne deux suites arithmétiques de raison r=1 : [|1;8|] et une de raison r=3, de 1er terme 2.
Au coup suivant , (nombre d'itérées k=2), ça donne quatre suites arithmétiques de raisons
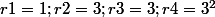
Au coup suivant , (nombre d'itérées k=3), ça donne huit suites arithmétiques de raisons
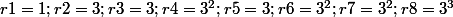
etc..
conclusionPour le graphe proposé par Bambino, il y a une formule explicite pour les sommes écrites en ordonnée,
quand
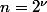
pour les

premières itérées.
Ensuite le comportement des sommes est mathématiquement obscur, car les valeurs initiales
des
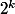
suites arithmétiques se périodisent "petit à petit" et l'on assiste à une décroissance exponentielle des sommes.
Amha, cette description introduit , dans le désordre Collatz, un ordre, une structure
fait
d'un arbre binaire de suites arithmétiques.
olivier bertrand

