Ou en sont les math?

[annick]

Bonjour,
personnellement, je n'ai pas les compétences pour répondre à tes questions, mais je trouve que tu as une bien belle approche de ta relation avec les maths.

[Mateo_13]

Bonjour lazare,

si tu cherches à faire des maths en autodidacte, une des meilleure source de problèmes et de méthodes pour les résoudre sont les livres de George Polya :
https://fr.shopping.rakuten.com/search/george+polya

Un site pour connaître l'actualité des Maths, de manière lisible :
https://images.math.cnrs.fr/

Amicalement,

[Mateo_13]

J'ai lu tous ses livres sur l'enseignement de la résolution de problèmes.

Polya est un grand chercheur, qui à fait la liste des bonnes questions à se poser pour résoudre un problème :

toutes les hypothèses (ce que l'on sait au départ) sont-elles indispensables ?
Peut-on en résoudre un cas particulier ? Peut-on généraliser le problème ?
Peut-on s'inspirer d'un problème similaire ? etc...

Polya illustre sa méthode par de nombreux problèmes accessibles en lycée et même avant,
sauf pour les deux tomes qu'il a écrit avec Szegö, qui sont de niveau L3.

La lecture de Polya devrait être recommandée à tous les étudiants en Maths.

Amicalement,

[Mateo_13]

Tu y trouveras des problèmes intéressants.

[Mateo_13]

Salut Lazare,

quand j'étais en 2nde, j'ai découvert en autodidacte ce que j'ai su plus tard qu'on appelait les différences finies.

J'ai observé que la suite des carrés des entiers (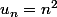) avait des écarts de plus en plus grands, donc j'ai envisagé la suite des écarts de deux termes consécutifs (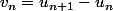), j'ai vu qu'elle croissait moins vite, donc j'ai continué : 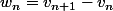et j'ai obtenu la suite constante égale à 2, ce qui m'a surpris.

J'ai voulu voir ce qui se passait avec la suite des cubes des entiers, puis des puissances 4 des entiers, etc... et j'ai conjecturé qu'au bout d'un nombre fini d'étapes, pour les puissances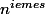 on aboutissait à , ce que j'ai démontré par de longs calculs.

Si on considère que les différences de termes consécutifs sont une approximation de la dérivée, j'ai découvert avant l'heure que la dérivé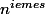e de était , et ce fut la fin de mon expérience d'autodidacte, et mon meilleur souvenir mathématique.

Amicalement,

[Mateo_13]

Polya est un des seuls mathématiciens qui a donné les clés de sa réflexion sur des problèmes ouverts en Maths, et tous ses lecteurs, dont moi, lui en sommes reconnaissants.

Je ne développerai pas davantage, et je te remercie d'avoir posté ce sujet, qui m'a permis d'en parler, et j'espère que de nouveaux lecteurs de Polya vont en découler.

Amicalement,

[Mateo_13]

Très élégant, lazare

[ComeDuRondeau]

Hello,

Le mieux que je puisse dire c'est qu'à mon sens aucun·e mathématicien·ne au monde ne sait "où en sont les math". Les maths c'est devenu trop vaste. Si Poincaré savait tout ce qu'il faut savoir des mathématiques à son époque c'est probablement un des seuls. Maintenant, il a des centaines de milliers de mathématicien·nes dans le monde qui travaillent sur des sujets ultra-spécifiques. Des centaines d'articles sont publiés tous les jours. Des dizaines de théories émergent chaque année. Des milliers de livres sont écrits tous les ans. Au mieux un·e mathématicien·ne peut savoir où en sont les math dans son domaine. Mais il y a peu de chance qu'un·e géomètre algébriste sache où en est la conjecture de Riemann, ni qu'un·e analyste ait une idée de ce qui se passe dans le domaine des D-modules...

Chaque domaine voit aussi ses grands objectifs se réaliser ou des grandes questions, des belles conjectures émerger. Après 4 ans de doctorat je vois toujours mal où en est mon domaine. Il m'a fallu des années pour comprendre et approfondir le sujet sur lequel je travaille et, si je continuais, il me faudrait probablement 10 ans de plus, à rencontrer, discuter, travailler, collaborer, pour avoir une vue d'ensemble cohérente sur le domaine que j'étudie.

Donc je pense que c'est assez téméraire d'espérer de savoir où en est la connaissance en mathématiques.

[azf]

...à mon sens aucun·e mathématicien·ne au monde ne sait "où en sont les math". ... Après 4 ans de doctorat...

Malgré vos années de doctorat, il sera quand même difficile pour vous de comprendre cette sentence écrite ci-dessous (La raison de cela est que votre charabia en novlangue n'est pas anodin)

Préparez-vous à vivre dans un monde empli de prisons invisibles, un monde de fausses libertés, dénué de culture et de civilisation, un monde d'hommes à tête sans visage.
Dans ce monde nouveau, ce qu'un homme pourra faire à un autre homme appartiendra au domaine de l'impensable.
Et le prix à payer pour penser et agir par soi-même sera le plus élevé de toute l'histoire de l'humanité

[lyceen95]

Les représentations de l'espace ???
Les fractales spatiaux ???
Les définitions des nombres ???